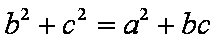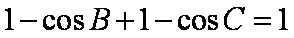- 三角函数的概念、同角三角函数的关系式和诱导公式
- 共714题
某观测站C在城A的南偏西25°的方向上,由A城出发有一条公路,走向是南偏东50°,在C处测得距C为
正确答案
见解析。
解析
根据题意得,BC=
设∠ACD=α,∠CDB=β
在△CDB中,由余弦定理得

于是
答:此人还得走
知识点
在△ABC中,若

正确答案
1
解析
由


知识点
在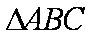
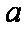
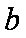
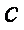
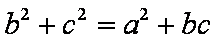
(1)求角A的大小:
(2)若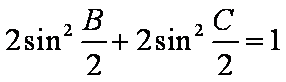
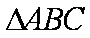
正确答案
见解析。
解析
(1)在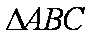
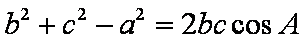
∴
(2)∵
∴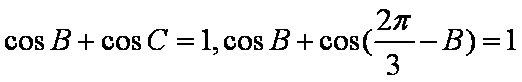
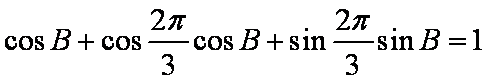
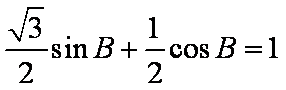
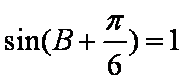
∵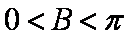
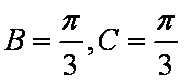
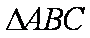
知识点
在△ABC中,角A、B、C所对的边分别为a、b、c,若
正确答案
解析
由


知识点
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上。
(1)怎样截取才能使截得的矩形ABCD的面积最大?并求最大面积;
(2)若将所截得的矩形铝皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),应怎样截取,才能使做出的圆柱形形罐子体积最大?并求最大面积。
正确答案
见解析
解析
(1)
(方法一)连结
设


则

所以
当且仅当



答:取


(方法二)连结



则

所以S=AB·BC=2OB·BC=900sin
所以当



答:取


(2)(方法一)设圆柱底面半径为


由

所以

由

因此


所以当


答:取

(方法二)连结



则圆柱的底面半径为


所以
设



因此


所以当



答:取

知识点
如果一个三角形的三边长度是连续的三个自然数,且最大角是最小角的两倍,该三角形的周长是 。
正确答案

解析
设三角形的三边长分别是










知识点
在△ABC中, AB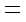
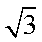
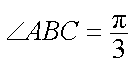
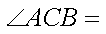
正确答案
解析
由正弦定理知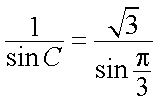
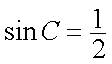

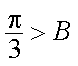
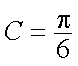
知识点
已知某四面体的六条棱长分别为





角的余弦值为 ▲ 。
正确答案
解析



知识点
在△ABC中,a、b、c分别为三内角A、B、C所对边的边长,且若是


(1)若

(2)若


正确答案
见解析
解析
由正弧定理得
则
则


若


若

(2)
又
由余弧定理知
即
故
即
知识点
已知O为坐标原点,点A的坐标是



正确答案
解析
先求出三条直线




如图所示的










知识点
扫码查看完整答案与解析