古典概型与几何概型
共235题

古典概型与几何概型
共235题

热门试卷

题型：简答题

简答题 · 14 分

20、（本题满分14）

有一块正方形菜地,所在直线是一条小河，收货的蔬菜可送到点或河边运走。于是，菜地分为两个区域和，其中中的蔬菜运到河边较近，中的蔬菜运到点较近，而菜地内和的分界线上的点到河边与到点的距离相等，现建立平面直角坐标系，其中原点为的中点，点的坐标为（1,0），如图

（1）求菜地内的分界线的方程

（2）菜农从蔬菜运量估计出面积是面积的两倍，由此得到面积的“经验值”为。设是上纵坐标为1的点，请计算以为一边、另一边过点的矩形的面积，及五边形的面积，并判断哪一个更接近于面积的经验值

正确答案

2.五边形EOMGH的面积更接近Ｓ１的面积　　　

解析

知识点

生活中的几何概型问题

题型：简答题

简答题 · 14 分

20.（本题满分14分）

有一块正方形菜地, 所在直线是一条小河，收货的蔬菜可送到点或河边运走。于是，菜

地分为两个区域和，其中中的蔬菜运到河边较近，中的蔬菜运到点较近，而菜地内和

的分界线上的点到河边与到点的距离相等，现建立平面直角坐标系，其中原点为的中点，

点的坐标为，如图

(1) 求菜地内的分界线的方程(2) 菜农从蔬菜运量估计出面积是面积的两倍，由此得到面积的“经验值”为。设是上

纵坐标为的点，请计算以为一边，另一边过点的矩形的面积，及五边形的面积，并

判断哪一个更接近于面积的经验值

正确答案

(1) 设分界线上任一点为，依题意

可得

(2) 设，则

∴

∴设所表述的矩形面积为，则

设五边形面积为，则

∴五边形的面积更接近的面积

知识点

与面积、体积有关的几何概型生活中的几何概型问题

题型：单选题

单选题 · 5 分

4.某公司的班车在7:00，8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是

正确答案

知识点

生活中的几何概型问题

题型：单选题

单选题 · 5 分

甲、乙两位同学各拿出六张游戏牌，用作投骰子的奖品，两人商定：骰子朝上的面的点数为奇数时甲得1分，否则乙得1分，先积得3分者获胜得所有12张游戏牌，并结束游戏．比赛开始后，甲积2分，乙积1分，这时因意外事件中断游戏，以后他们不想再继续这场游戏，下面对这12张游戏牌的分配合理的是（）

A甲得9张，乙得3张

B甲得6张，乙得6张

C甲得8张，乙得4张

D甲得10张，乙得2张

正确答案

解析

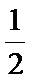
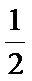
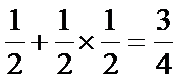
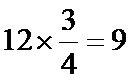
由解题思路可知，我们来分析接下来两局的情况：①接下来一局若出现奇数（概率为），则甲再得1分，此时甲已获胜；②接下来一局若出现偶数（概率为），乙得1分，甲、乙两人同分，接下来甲、乙获胜的概率一样；所以甲获胜的概率应为，故甲应该获得张游戏牌。故应该选A选项。

考查方向

本题主要考查了条件概率；高考常考独立事件的概率、排列组合在古典概型中的应用、几何概型和二项分布及超几何分布。

解题思路

由题设每局甲、乙两位得1分的概率相同均为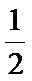，所以本题在甲积2分，乙积1分的前提下如何分配游戏牌应转化为在此条件下甲、乙获胜的概率。

易错点

解题思路不好寻找导致无法解出此题。

知识点

生活中的几何概型问题

题型：简答题

简答题 · 13 分

李明在10场篮球比赛中的投篮情况如下（假设各场比赛互相独立）：

（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过的概率.

（2）从上述比赛中选择一个主场和一个客场，求李明的投篮命中率一场超过，一

场不超过的概率.

（3）记是表中10个命中次数的平均数，从上述比赛中随机选择一场，记为李明

在这比赛中的命中次数，比较与的大小（只需写出结论）.

正确答案

见解析。

解析

(1)根据投篮统计数据，在10场比赛中，李明投篮命中率超过0.6的场次有5场，分别是主场2，主场3，主场5，客场2，客场4.

所以在随机选择的一场比赛中，李明的投篮命中率超过0.6的概率是05.

（2）设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”，

事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”，

事件C为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6”。

则C=，A,B独立。

根据投篮统计数据，.

，

所以，在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6的概率为.

（3）.

知识点

生活中的几何概型问题

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 二项分布与正态分布

百度题库 > 高考 > 理科数学 > 古典概型与几何概型

扫码查看完整答案与解析