- 二项分布与正态分布
- 共188题
一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同)。
(1)求取出的4张卡片中,含有编号为3的卡片的概率;
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望。
正确答案
(1) 




解析
(1)设“取出的4张卡片中,含有编号为3的卡片”为事件A,则
P(A)=
所以,取出的4张卡片中,含有编号为3的卡片的概率为
(2)随机变量X的所有可能取值为1,2,3,4.
P(X=1)=
P(X=2)=
P(X=3)=
P(X=4)=
所以随机变量X的分布列是
随机变量X的数学期望EX=1×




知识点
从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=( )
正确答案
解析
知识点
甲、乙两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次不同视为不同情形)共有( )
正确答案
解析
两人比赛局数为3局、4局或5局.当局数为3时,情况为甲或乙连赢3局,共2种;当局数为4时,若甲胜,则甲第4局胜,且前3局胜2局,有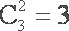
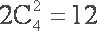
知识点
从1.2.3.4.5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=( )
正确答案
解析
事件A=“取到的2个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(3,5)、(2,4),
∴p(A)=
事件B=“取到的2个数均为偶数”所包含的基本事件有(2,4),∴P(AB)=
∴P(B|A)=
故选B。
知识点
5位同学报名参加甲和乙两个课外小组,每位同学都要报名且限报1个,且甲小组至少有2名同学报名,乙小组至少有1名同学报名,则不同的报名方法有( )
正确答案
解析
对甲组有2人,3人,4人分类 

选A
知识点
采用系统抽样方法从1000人中抽取50人做问卷调查,为此将他们随机编号为1,2,…,1000,适当分组后在第一组采用简单随机抽样的方法抽到的号码为8,抽到的50人中,编号落入区间[1,400]的人做问卷A,编号落入区间[401,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为
正确答案
解析
略
知识点
有甲、乙、丙三人到某公司面试,甲、乙通过面试的概率分别为


(1)求
(2)求至少有两人通过面试的概率;
(3)求数学期望EX.
正确答案
见解析
解析
设 “甲通过面试”为事件


所以


(1)由已知得

所以
(2)设“至少有两人通过面试”为事件
由题意知
所以 
(3)由题意得
所以
………………………… 13分
知识点
若甲乙两人从


正确答案
答案:180
解析
略
知识点
某医务人员说:“包括我在内,我们社区诊所医生和护士共有16名,无论是否把我算在内,下面说法都是对的,在这些医务人员中:护士多于医生;女医生多于女护士;女护士多于男护士;至少有一名男医生,”请你推断说话的人的性别与职业是( )
正确答案
解析
设男护士人数为a,女护士人数为b,男医生人数为c,女医生人数为d
则有:
(一)a+b>c+d
(二)c>a
(三)a>b
(四)d≥1
得出:c>a>b>d≥1
假设:d=1
仅有:a=5,b=4,c=6,d=1时符合条件,
又因为使abcd中一个数减一任符合条件,只有d,即女医生
假设:d>1
则没有能满足条件的情况
综上,这位说话的人是女医生,
故选:C
知识点
选聘高校毕业生到村任职,是党中央作出的一项重大决策,这对培养社会主义新农村建设带头人、引导高校毕业生面向基层就业创业,具有重大意义。为了响应国家号召,某大学决定从符合条件的6名(其中男生4人,女生2人)报名大学生中选择3人,到某村参加村委会主任应聘考核。
(1)设所选3人中女生人数为

(2)在男生甲被选中的情况下,求女生乙也被选中的概率。
正确答案
见解析。
解析
(1)
依题意得:


∴
∴ 
(2)设“男生甲被选中”为事件

则

∴
故在男生甲被选中的情况下,女生乙也被选中的概率为
知识点
扫码查看完整答案与解析




















