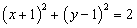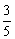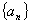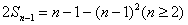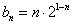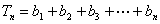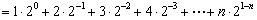- 集合的含义
- 共388题
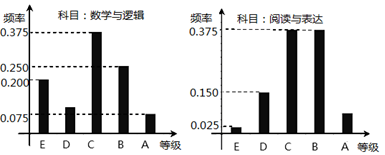
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为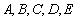
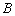
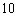
(1)求该考场考生中“阅读与表达”科目中成绩为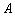
(2)若等级
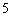
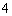
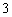
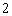
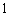
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为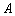
正确答案
见解析。
解析
(1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有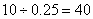
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为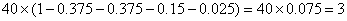
(2)该考场考生“数学与逻辑”科目的平均分为
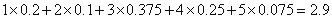
(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为
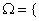
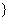
设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则
知识点
已知点




右焦点


(1)求椭圆
(2)已知点









(3)作直线










正确答案
见解析。
解析
(1)由题意知,在
由
设


因为
又



因为点


又
所求椭圆

(2)由(1)知椭圆
由题意知直线

则其方程为
设


又

解得
所以直线


(3)由题意知: 
由
根据题意可知直线


把它代入椭圆

由韦达定理得

所以线段
(1)当



于是
由

(2) 当

因为点

令
于是
由
代入
综上, 满足条件的实数


知识点
以点(-1,1)为圆心且与直线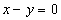
正确答案
解析
略
知识点
已知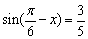
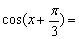
正确答案
解析
略
知识点
在数列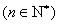
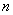
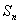
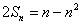
(1)求数列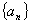
(2)设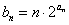
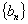
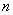
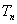
正确答案
见解析。
解析
(1)由题设得: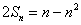
所以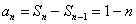
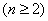
当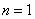
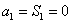
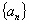
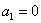
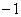
故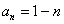
(2)由(1)知:
所以
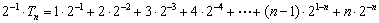
两式相减得:
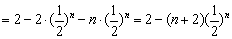
所以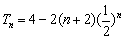
知识点
扫码查看完整答案与解析