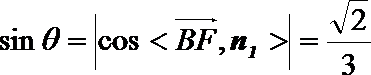- 平面与平面垂直的判定与性质
- 共123题
1
题型：简答题
|
18．如图，四棱锥
（1）求证：平面
（2）当
（3）在（2）的条件下若F是PD的靠近P的一个三等分点，求二面角A-EF-D的余弦值．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
棱柱、棱锥、棱台的体积直线与平面垂直的判定与性质平面与平面垂直的判定与性质线面角和二面角的求法
1
题型：简答题
|
17．三棱锥P−ABC中，PA⊥平面ABC，AB⊥BC。
（1）证明：平面PAB⊥平面PBC；
（2）若PA=，PC与侧面APB所成角的余弦值为，PB与底面ABC成60°角，求二面角B―PC―A的大小。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
平面与平面垂直的判定与性质
1
题型：
单选题
|
6．下列命题正确的是（ ）
A若两个平面分别经过两条平行直线，则这两个平面平行
B若平面
C平行四边形的平面投影可能是正方形
D若一条直线上的两个点到平面
正确答案
C
解析
解析已在路上飞奔，马上就到！
知识点
命题的真假判断与应用平行投影及平行投影作图法直线与平面平行的判定与性质平面与平面平行的判定与性质平面与平面垂直的判定与性质
1
题型：简答题
|
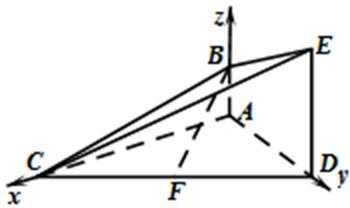
19．已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等腰直角三角形，AC⊥AD，且AD=DE=2AB，F为CD中点。
（Ⅰ）求证：平面BCE⊥平面CDE；
（Ⅱ）求直线BF和平面BCE所成角的正弦值。
正确答案
以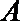
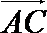
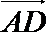
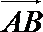
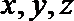
设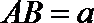
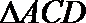
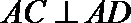
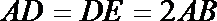
所以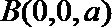
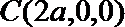
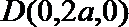
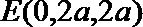
所以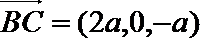
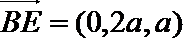
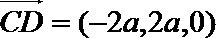
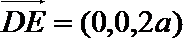
（Ⅰ）设平面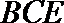
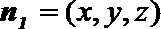
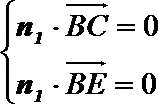
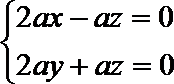
令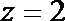
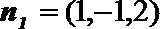
设平面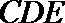
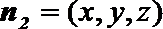
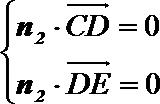
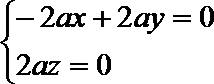
令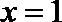
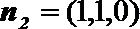
所以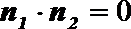
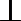
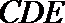
（Ⅱ）因为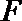
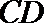
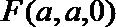
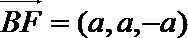
则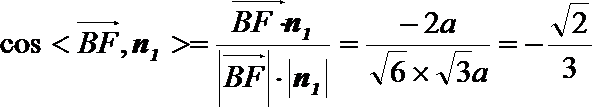
设直线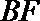
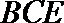
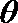
所以直线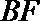
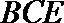
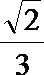
解析
解析已在路上飞奔，马上就到！
知识点
平面与平面垂直的判定与性质用空间向量求直线与平面的夹角
1
题型：简答题
|
19．如图，
（1）若
（2）求平面
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
直线与平面平行的判定与性质平面与平面垂直的判定与性质线面角和二面角的求法
下一知识点 : 直线、平面垂直的综合应用
扫码查看完整答案与解析