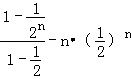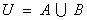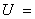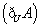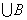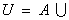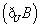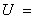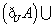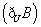- 判断两个函数是否为同一函数
- 共19题
已知函数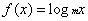
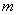
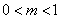
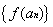
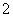
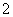
(1)若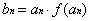
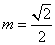
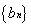
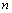
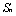
(2)设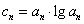
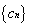
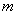
正确答案
见解析。
解析
(1)由题意得f(an)=2+2(n﹣1)=logman,可得2n=logman,
∴an=m2n。…(2分)
bn=an•f(an)=2n•m2n。
∵m=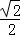
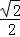
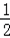
∴Sn=1•(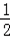
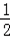
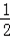
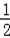
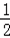
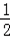
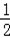
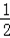
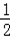
①﹣②,得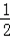
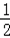
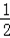
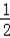
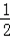
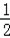
∴化简得:Sn=﹣(n+2)(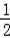
(2)解:由(1)知,cn=an•lgan=2n•m2nlgm,要使cn<cn+1对一切n∈N*成立,
即nlgm<(n+1)m2lgm对一切n∈N*成立。
∵0<m<1,可得lgm<0
∴原不等式转化为n>(n+1)m2,对一切n∈N*成立,
只需m2<(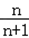
∵h(n)=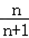
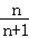
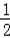
∴m2<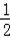
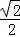
综上所述,存在实数m∈(0,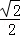
知识点
设函数
(1)求函数
(2)当



正确答案
见解析。
解析
(1)
则

且当

即

(2)当




所以


知识点
下列四个函数中,既是奇函数又在定义域上单调递增的是()
正确答案
解析
略
知识点
设全集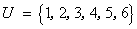
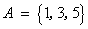
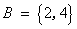
正确答案
解析
略
知识点
已知函数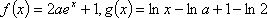

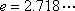
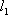
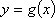
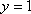
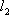
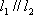
(1)若在闭区间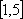

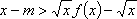
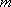
(2)对于函数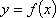
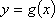
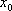
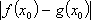
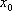
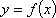
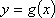
正确答案
见解析
解析
(1)函数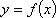
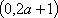
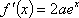
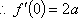
函数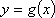
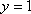
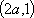
又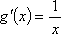
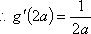
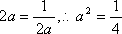
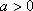
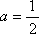
不等式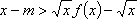
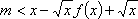
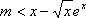
令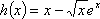
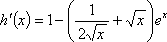
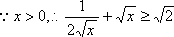
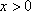
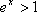
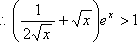
故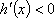
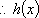
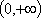
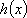
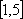
因此,在闭区间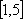

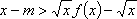
只需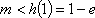
所以实数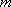
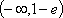
(2)证明: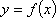
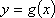
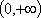
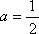
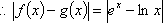
令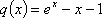
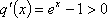
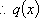
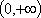
故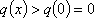
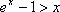
令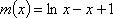
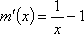
当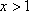
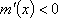
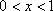
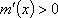
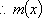
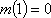
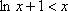
由①②得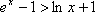
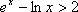
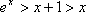
由②得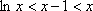
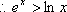
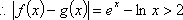
故函数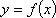
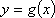
知识点
扫码查看完整答案与解析