- 三角形中的几何计算
- 共100题
16.在△ABC中,角A、B、C所对的边分别为a、b、c, q=(



(1)求sin A的值;
(2)求三角函数式
正确答案
解:(1)∵

根据正弦定理,得
又



又
(2)原式

∵

∴
∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
13.已知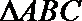
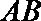
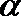
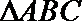
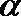
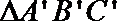
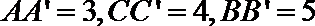
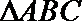
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在△ABC中, 

正确答案
解析
因为
所以
代入tan B=3tan C,
可得
解得t 
则
知识点
19.如图,在△ABC中,

(1)求BC的长;
(2)求△DBC的面积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知菱形






正确答案
2
解析


考查方向
解题思路
本题考查运用平面向量在几何中的应用,解题步骤如下:建立如图所示直角坐标系,
则

易错点
本题必须注意审题,忽视则会出现错误。
知识点
15. 已知在



正确答案
解析
因为



考查方向
解题思路
由正弦定理整理,二倍角正弦公式
易错点
正弦定理的转化
知识点
16.在△ABC中,角A、B、C的对边分别为a、16.在△ABC中,角A、B、C的对边分别为a、b、c,若2ccosB=2a+b,△ABC的面积为S=
正确答案
解析
在
即
再由余弦定理可得,
整理可得
即
考查方向
解题思路
本题主要考查了正余弦定理在解三角形中的应用及诱导公式和两角和的正弦公式、基本不

易错点
本题在化边为角的过程中易错
知识点
16.已知ΔABC为等边三角形,点M在ΔABC外,且MB = 2MC = 2,则MA的最大值是__________。
正确答案
3
解析
试题分析:如图,以M为坐标原点,建立坐标系,则B(2,0),设

又因为

由


考查方向
解题思路
建立坐标系,利用正余弦定理即可求MA的最大值。
易错点
不知如何建立坐标系,对已知条件不知如何应用导致本题无思路。
知识点
15.在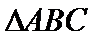
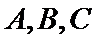
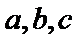
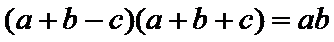
(1)求角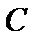
(2)若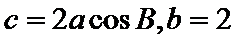
正确答案
(1)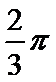
(2)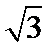
解析
试题分析:本题属于解三角形中的基本问题,难度不大。
(1)此类问题主要应用正(余)弦定理和三角形面积公式;
(2)注意边和角的统一。
解析:(1)在△ABC中,由(a+b-c)(a+b+c)=ab,得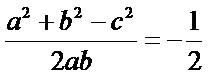
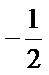
因为0<C<π,所以C=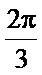
(2)因为c=2acosB,由正弦定理,得
sinC=2sinAcosB,
因为A+B+C=π,所以sinC=sin(A+B),
所以sin(A
又-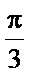
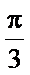
所以A-B=0,即A=B,所以a=b=2.
所以△ABC的面积为S△ABC=absinC=×2×2×sin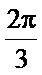
考查方向
本题旨在考查三角函数的基本关系、正弦定理、余弦定理、三角形面积公式、向量的数量积等基本知识,考查运算求解能力.难度较小.
解题思路
本题旨在考查三角函数的基本关系、正弦定理、余弦定理、三角形面积公式、向量的数量积等基本知识.
解题步骤如下:
化简已知条件,利用余弦定理求解。
边角互化,利用正(余)弦定理和三角形面积公式求解。
易错点
第一问中化简易出错误。
第二问不知道统一成边或者角进行处理。
知识点
10.某小组共有8名同学,其中男生6人,女生2人,现从中按性别分层随机抽4人参加一项公益活动,则不同的抽取的方法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析





















