三角形中的几何计算_章节学习

1

题型：简答题

|

简答题 · 12 分

函数.

16.求函数的最大值；

17.若且，求的值.

第(1)小题正确答案及相关解析

正确答案

见解析

解析

考查方向

本题主要考察了向量的数量积运算，考察了两角和的正弦、余弦公式，考察了特殊角的三角函数值，属于常见题型，比较简单

解题思路

该题解题思路如下利用数量积运算，得出

使用和角公式化简解析式成一角一函数，进而求出最大值

易错点

该题易于在角的范围上判断出错，

第(2)小题正确答案及相关解析

正确答案

见解析

解析

考查方向

本题主要考察了向量的数量积运算，考察了两角和的正弦、余弦公式，考察了特殊角的三角函数值，属于常见题型，比较简单

解题思路

该题解题思路如下

根据正弦值和角的范围求余弦值

利用凑角的方式和两角和的余弦公式得到答案，

易错点

该题易于在角的范围上判断出错，

1

题型：单选题

|

单选题 · 5 分

5.中，角所对的边分别为，若（）．

A

B

C

D

正确答案

C

解析

由余弦定理，又由，得，故选C．

考查方向

本题主要考查余弦定理和已知三角函数值求角等知识，意在考查考生的运算求解能力和转化与化归的能力。

解题思路

1.先根据余弦定理求出角A的余弦值；

2.利用特殊角的三角函数值求出角A的大小。

易错点

1.对于余弦定理的公式记忆错误；

2.对于特殊角的三角函数值记忆出错。

知识点

三角形中的几何计算

1

题型：简答题

|

简答题 · 14 分

在中，角的对边分别是，且向量与向量共线.

16.求；

17.若，且，求的长度.

第(1)小题正确答案及相关解析

正确答案

解析

解：与共线，

在三角形中，

……………………………………………………7分

考查方向

考查向量的共线，考查三角函数的恒等变换，考查解三角形余玄定理的应用

解题思路

先通过共线，列出方程，然后用正弦定理，将边转成角，用利用和角公式，先用余弦定量得到a的方程，为求BD的模，可以通过平方再开方的办法间接的模。

易错点

对向量共线掌握不准，对三角恒等变换及正余定理的应用不熟练

第(2)小题正确答案及相关解析

正确答案

解析

解：且

即

解得（舍）……………………………………………9分

将和代入得：

……………………………………………14分

考查方向

考查向量的共线，考查三角函数的恒等变换，考查解三角形余玄定理的应用

解题思路

先通过共线，列出方程，然后用正弦定理，将边转成角，用利用和角公式，先用余弦定量得到a的方程，为求BD的模，可以通过平方再开方的办法间接的模。

易错点

对向量共线掌握不准，对三角恒等变换及正余定理的应用不熟练

1

题型：填空题

|

填空题 · 5 分

13．在ABC中，B=，AB=，A的角平分线AD=,则AC=_______.

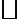
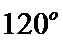
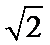
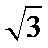
正确答案

解析

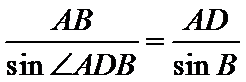
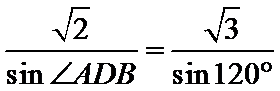
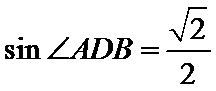
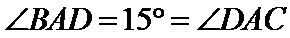
由正弦定理得，即，解得

，，从而，

所以，.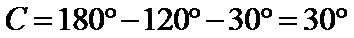

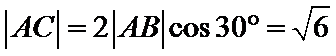
考查方向

解三角形（正弦定理，余弦定理）

解题思路

解三角形就是根据正弦定理和余弦定理得出方程进行的．当已知三角形边长的比时使用正弦定理可以转化为边的对角的正弦的比值，本例第一题就是在这种思想指导下求解的；当已知三角形三边之间的关系式，特别是边的二次关系式时要考虑根据余弦定理把边的关系转化为角的余弦关系式，再考虑问题的下一步解决方法．

易错点

边角关系的转化

知识点

正弦定理的应用三角形中的几何计算

1

题型：单选题

|

单选题 · 5 分

6．在中，，则=（）

A-1

B1

C

D-2

正确答案

A

解析

,可得，

,因为A、B都小于45度，所以C为钝角，所以

考查方向

同角三角函数间的基本关系

解题思路

根据所给条件，求出其他同角三角函数值

易错点

计算错误，忽略取值正负

知识点

正弦定理余弦定理三角形中的几何计算

热门试卷

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点