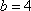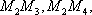- 空间点、线、面的位置关系
- 共260题
已知正方体

正确答案
解析
取A1B1的中点M连接EM,AM,AE,则


知识点
(1-3x)5的展开式中x3的系数为( )
正确答案
解析
(1-3x)5的展开式的通项为Tr+1=

知识点
设双曲线的左准线与两条渐近线交于

正确答案
解析
设双曲线为



以AB为直径的圆:



即

知识点
设函数
(1)求
(2)若函数


求

正确答案
(1) 
解析
(1)
故
(2)依题意
当
所以
知识点
如图,几何体








(1)求异面直线

(2)求几何体
正确答案
见解析
解析
(1)解法一:在



由题意得,



∴




∵ 

∴
∴
则

所成的角.
由平面几何知识及勾股定理可以得
在

∵ 异面直线的夹角范围为
∴ 异面直线


解法二:
同解法一得


分别为
可得
∴ 
得
设向量


∵ 异面直线的夹角范围为
∴ 异面直线


(2)
如图,连结





∵

∴ 几何体
知识点
在长方体






(1)求异面直线
(2)求以
正确答案
(1)
解析
联结


又

∴

由

∴


(2)由题意可知,点


∴
∵
∴
知识点
把正方形ABCD沿对角线BD折成直二面角,对于下面结论:①AC⊥BD;②CD⊥平面ABC;③AB与BC成600角;④AB与平面BCD成450角。则其中正确的结论的序号为
正确答案
解析
略
知识点
如图,四棱锥



(1)求证:
(2)求异面直线

正确答案
见解析
解析
(1)∵

∴CD⊥SD
又四边形ABCD是正方形,∴CD⊥AD
∴CD⊥平面SDA

∴SA⊥CD.
(2)∵
∴


由(1),BA⊥平面SDA,∴△SAB是直角三角形.

故异面直线SB与CD所成角的大小为
知识点
某单位从一所学校招收某类特殊人才,对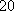
例如表中运动协调能力良好且逻辑思维能力一般的学生是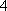
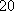

(1)求
(2)从运动协调能力为优秀的学生中任意抽取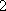
正确答案
(1)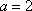
(2)
解析
(1)由题意可知,逻辑思维能力优秀的学生共有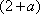
设事件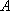
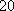
则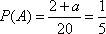
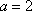
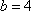
(2)由题意可知,运动协调能力为优秀的学生共有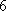
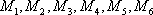
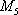
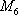
从中任意抽取
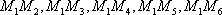
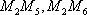
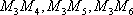
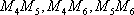
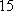
设事件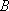
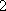
事件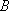
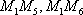
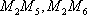
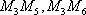
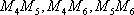
所以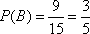
所以至少有一位逻辑思维能力优秀的学生的概率为
知识点
已知正方体

(1)求异面直线

(2)求四棱锥
正确答案
(1)
解析
(1)因为 





又




(2)四棱锥
知识点
扫码查看完整答案与解析