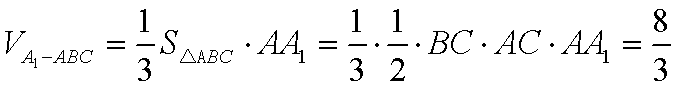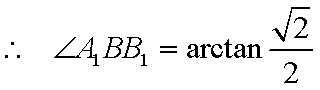- 空间点、线、面的位置关系
- 共260题
如图,四面体







(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)因为CO=

(2)因为O、E为中点,所以OE//CD,所以
AE与CD所成角。
在直角三角形AEO中,
知识点
如图,三棱柱



(1)求异面直线

(2)证明:平面

正确答案
见解析
解析
(1)由题设知AA1//BB1,
所以异面直线DC1和BB1所成的角为
因为侧棱垂直底面,

又AC=BC=AA1,D是棱AA1的中点,


所以,异面直线


(2)由题设知
又
由题设知

又



知识点
在棱长为





(1)求异面直线

(1)求三棱锥
正确答案
(1)
解析
解析:(1)由题意得


计算


(2)

所以


知识点
如图,已知点








(1)求三棱锥
(2)求异面直线

正确答案
(1)
解析
解析:(1)由题意

在△


在△


所以
(2)取




得


又



由余弦定理得
所以异面直线


知识点
如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点,求证:
(1)PA∥平面MDB;
(2)PD⊥BC。
正确答案
见解析。
解析
(1)
连接AC,交BD与点O,连接OM,
∵M为PC的中点,O为AC的中点,
∴MO∥PA,
∵MO⊂平面MDB,PA⊄平面MDB,
∴PA∥平面MDB。
(2)∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC⊂平面ABCD,BC⊥CD,
∴BC⊥平面PCD,
∵PD⊂平面PCD,
∴BC⊥PD。
知识点
重庆市教委为配合教育部公布高考改革新方案,拟定在重庆彳中学进行调研,广泛征求高三年级学生的意见,重庆么中学高三年级共有700名学生,其中理科生500人,文科生200人,现采用分层抽样的方法从中抽取14名学生参加调研,则抽取的理科生的人数为
正确答案
解析
抽样比例为:

故答案为:D
知识点
如图,四棱锥







(1)证明:
(2)证明:

正确答案
见解析。
解析
(1)由



又

(2)
取




又


所以

知识点
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形。
(1)求证:PC⊥BD;
(2)试在线段PD上确定一点E,使得PB//面ACE;
(3)求这个简单多面体的表面积。
正确答案
见解析
解析
(1)连接BD,∵俯视图ABCD是正方形 ∴ BD
又PA 

PA



(2)存在点E是PD的中点使PB∥面ACE,连接BD交于点O,连接EO.
∵EO∥PB, EO
∴PB∥面PEC (8分)
(3)S△PAB= S△PAD=

∵BC⊥BA BC⊥PA
∴BC⊥面PAB
∴BC⊥PB, S△PBC=



同理S△PDC=


∴S表= S△PAB+ S△PAD+ S四ABCD+S△PBC+S△PDC=




知识点
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5. 点D是AB的中点,
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
(3)求异面直线 AC1与 B1C所成角的余弦值。
正确答案
见解析。
解析
(1)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴ AC⊥BC,
又因为 
又 





(2)
设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点
∵ DE


(3)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
在△CED中,ED=





∴ 
∴ 异面直线 AC1与 B1C所成角的余弦值
知识点
如图,在直三棱柱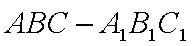
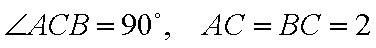
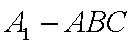
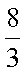
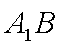
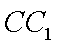

正确答案
见解析
解析
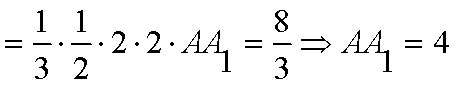
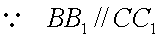
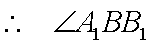
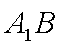
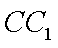
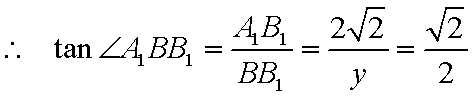
所以直线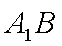
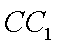
知识点
扫码查看完整答案与解析