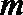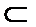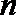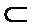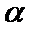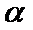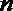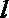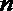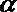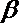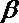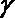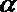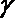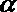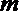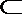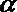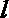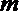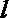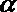- 空间点、线、面的位置关系
- 共260题
8.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a⊥c;
③若a∥γ,b∥γ,则a∥b;
④若a⊥γ,b⊥γ,则a∥b.
其中真命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设

①
②
③
④
其中正确命题的个数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知


①若

②若

③若

④若

其中正确的命题是(填上所有正确命题的序号)( ).
正确答案
① ④
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线



①若


②若


③若


④若


其中真命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设

①若


②若
③若
④若
其中正确命题的序号是______________(把所有正确命题的序号都写上).
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
7.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.直线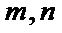
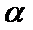
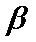
①若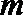
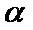
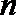

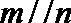
②若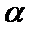
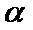
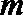
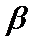
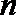
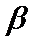
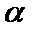
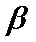
③若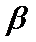
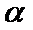
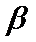
④若
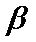
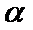
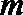

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设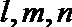
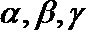
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.两个面垂直,经过第一个面内一点且垂直于交线的直线( )
正确答案
解析
因为经过第一个面内一点且垂直于交线的直线有三种情况,分别是与第二个平面垂直、相交、平行,所以选D.
知识点
19.如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.
(Ⅰ)求证:AB1⊥BC;
(Ⅱ)若AB⊥AC,AB1=BB1,且该三棱柱的体积为2
正确答案
(Ⅰ)略(Ⅱ)AB=2
解析
(Ⅰ) 取BC的中点M,连接AM,B1M.
因为AB=AC, M是BC的中点,所以AM⊥BC
又因为侧面BB1C1C是菱形,且∠B1BC=60°
所以B1M⊥BC,
而AM∩B1M=M , AM, B1M
所以BC⊥平面AB1M,因为A B1
所以BC⊥AB1
(Ⅱ) 设AB=

因为 M是BC的中点,所以
又因为AB1=BB1, 所以
由(Ⅰ)知 B1M⊥BC,且AM∩BC=M,所以B1M⊥平面ABC,
即B1M为三棱柱ABC--A1B1C1的高,
所以三棱柱ABC--A1B1C1的体积V=Sh=
解得
考查方向
解题思路
解题步骤如下:在本题中,要证明两条异面直线垂直,需要证明一条直线垂直于另一条直线所在的平面,即需要线面垂直,即可得到线线垂直。根据题目给出的条件,知道体积,要求线段AB的长,联想到体积等于底面积乘以高,自然而然要去证明B1M为三棱柱ABC--A1B1C1的高,即可求出线段AB的长。
易错点
1、本题易在证明线面垂直时发生错误 。2、本题不容易得出B1M为三棱柱ABC--A1B1C1的高,导致题目无法进行。
知识点
扫码查看完整答案与解析