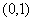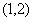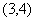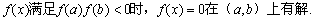- 函数与方程
- 共186题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数f(x)=
正确答案
解析
当a=0时,f(x)=
∴b∈[0,1]时,f(b)∈[1,
∴f(f(b))≥
∴不存在b∈[0,1]使f(f(b))=b成立,故D错;
当a=e+1时,f(x)=
∴f(f(1))=f(0),显然无意义,故B,C错,故选A。
知识点
用二分法求方程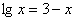
正确答案
解析
设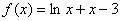
当连续函数
知识点
设函数




正确答案
解析
方法一:在同一坐标系中分别画出两个函数的图象,要想满足条件,则有如图,做出点A关于原点的对称点C,则C点坐标为


方法二:设


















知识点
已知函数f(x)=axsinx-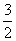
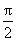
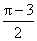
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,π)内的零点个数,并加以证明。
正确答案
(1) f(x)=xsinx-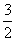
解析
(1)由已知得f′(x)=a(sinx+xcosx),
对于任意x∈(0,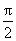
当a=0时,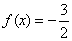
当a<0,x∈(0,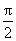
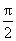
又f(x)在[0,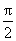
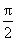
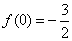
当a>0,x∈(0,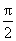
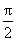
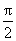
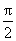
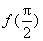
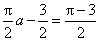
解得a=1。
综上所述,得f(x)=xsinx-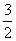
(2)f(x)在(0,π)内有且只有两个零点。
证明如下:
由(1)知,f(x)=xsinx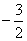
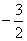
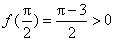
又f(x)在[0,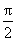
所以f(x)在(0,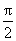
又由(1)知f(x)在[0,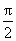
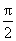
当x∈[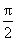
由g(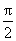
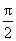
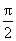
由g′(x)=2cosx-xsinx,知x∈(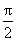
从而g(x)在(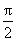
当x∈(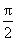
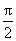
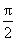
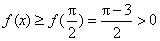
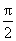
当x∈(m,π)时,有g(x)<g(m)=0,即f′(x)<0,从而f(x)在(m,π)内单调递减。
又f(m)>0,f(π)<0,且f(x)在[m,π]上的图象是连续不断的,从而f(x)在(m,π)内有且仅有一个零点。
综上所述,f(x)在(0,π)内有且只有两个零点
知识点
已知x是函数f(x)=2x+ 





正确答案
解析
选B,考察了数形结合的思想,以及函数零点的概念和零点的判断,属中档题
知识点
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣3x,则函数g(x)=f(x)﹣x+3的零点的集合为( )
正确答案
解析
∵f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣3x,
令x<0,则﹣x>0,
∴f(﹣x)=x2+3x=﹣f(x)
∴f(x)=﹣x2﹣3x,
∴
∵g(x)=f(x)﹣x+3
∴g(x)=
令g(x)=0,
当x≥0时,x2﹣4x+3=0,解得x=1,或x=3,
当x<0时,﹣x2﹣4x+3=0,解得x=﹣2﹣
∴函数g(x)=f(x)﹣x+3的零点的集合为{﹣2﹣
知识点
已知函数



正确答案
5
解析
方程















知识点
用二分法求方程
正确答案
解析
设
当连续函数
知识点
扫码查看完整答案与解析