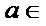- 函数与方程
- 共186题
8.已知a+b(a>0,b>0)是函数

正确答案
解析
1、由题可知,易得a+b=30-3a,即4a+b=30。
考查方向
解题思路
本题考查函数的零点及基本不等式,解题步骤如下:利用基本不等式求解即可
易错点
本题易在应用基本不等式的公式时发生错误。
知识点
8. 设函数
在


正确答案
解析
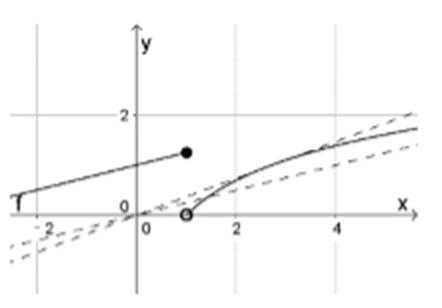
如图所示,
由题意可知,
可以令
即是

由此可以得到参数

所以选C
考查方向
解题思路
作出正确的图象,找到临界值
易错点
不能做出正确的图象,不理解函数零点的意思
知识点
21.设函数f(x)=

(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当m≥1时,讨论函数f(x)与g(x)图象的交点个数.
正确答案
(1)当






解析
(1)直接按照步骤来求;
(2)要注意对参数的讨论.
⑴解:函数


当



当




当


综上:当






⑵解:令

当

当

当





当












当













综上,函数
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论得结论。
易错点
第二问中的易丢对a的分类讨论。
知识点
12. 若函数

正确答案
解析
因为
所以
另
所以
所以可得


所以结合选项,b的取值范围为
考查方向
解题思路
先根据导函数在区间上有零点,得到b的取值范围,再利用b的取值范围,求出函数的单调区间,结合题目,选择正确的选项
易错点
判断b的取值范围,
知识点
12.已知函数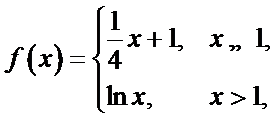
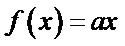
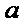
正确答案
解析
作出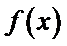
易知函数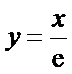
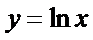
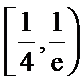
函数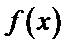
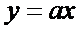
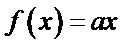
应选B.
考查方向
解题思路
1.画出分段函数的图象;
2.通过数形结合得出结果,应选B。
易错点
1.分段函数的图象不易画出;
2.识图能力较差,找不到里面的隐含条件。
知识点
15. 已知函数

正确答案
解析
考查方向
解题思路
该题信息量比较大关键在于理清解题思路
易错点
本题易错点有:1、图像画不出,2、关于
知识点
12.已知偶函数






正确答案
解析
由










考查方向
本题主要考查了函数的性质(奇偶性、周期性)和方程的根的个数。
易错点
本题易在时由

知识点
12.已知函数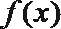
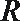
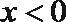
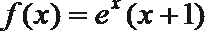
①当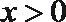
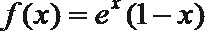
②函数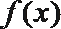
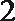
③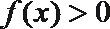
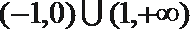
④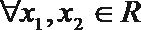
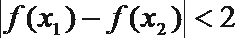
其中正确的命题是( )
正确答案
解析
当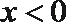
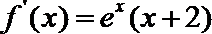
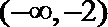
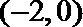
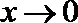
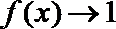
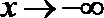
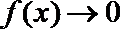
考查方向
本题主要考查函数的综合应用
解题思路
正确画出函数的图象。
易错点
1、函数性质理解不透;
2、不能正确的分析出函数的基本形式。
知识点
10.已知函数

正确答案
解析
画出函数
考查方向
本题主要考查了求分段函数的零点及数形结合思想,在近几年的各省高考题出现的频率较高,常与分段函数、函数图像变换等知识点交汇命题。
易错点
对集合的代表元素认识不清导致出错。
知识点
10.设函数f(x)=
正确答案
解析
试题分析:本题属于函数中的零点问题,题目的难度较大。注意对函数f(x)的值域的分析.
考查方向
本题主要考查了函数的零点问题,在近几年的各省高考题出现的频率较高,常与基本初等函数图像、不等式含参问题等知识点交汇命题。
解题思路
本题考查函数的零点问题,解题步骤如下:
由题可知,函数f(x)∈(-1,1), [f(x)]3+2∈(1,3), |f(x)|∈[0,1)。
故只有当a>3时,方程才有2个不等的实根。
易错点
本题易在含参的讨论上发生错误。
知识点
扫码查看完整答案与解析