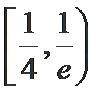- 函数与方程
- 共186题
21.已知函数
(I)讨论
(II)若
正确答案
II)解:由①知
若a≥0 f(x)在(-∞,1)减,(1,+∞)增,且f(1)=-e<0.
x→+∞时,f(x) →+∞,x→-∞时,f(x)→+∞
∴一定有2个零点;
若a<- 
且f(1)=-e<0 f(x)只有一个零点;
若a=- 
若0>a>
∵f(1)=-e<0 x→+∞时,f(x)→+∞,x→-∞时f(x) →-∞
∴f(x)在(1,+∞)内只有一个零点,f(x)若恰有2个零点,只能使f(ln(-2a)=0
而[ln(-2a)-2]·(-2a)+a[ln(-2a)-1]2=0
即须4-ln(-2a)+[ln(-2a)-1]2=0* ∵
∴4-ln(-2a)>0,[ln(-2a)-1]2>0 ∴*不可能为0
综上f(x)有2个零点 a的范围为[0,+ ∞]
知识点
15.已知函数f(x)=
正确答案
知识点
17.设


正确答案
知识点
14.若函数
正确答案
(-2,+∞)
考查方向
易错点
1.不注意指数函数的有界性导致出错;
知识点
13.设





正确答案
解析



则

则当x>1时,函数为增函数,且当x
当x 


由

考查方向
解题思路
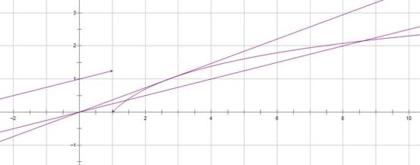
函数与方程的思想,将函数的零点转化为方程的解、两个函数的交点,用函数的图形来处理。
易错点
1、对零点概念、方程与函数的思想理解不到位,不能准确地转化为函数来处理。
2、本题不容易理解有且只有一个零点含义,从而造成求解上的不精确。。
知识点
13.函数
正确答案
解析
函数





考查方向
解题思路
画出图像转化为求图像交点的个数的问题。
易错点
不会用数形结合法做。
知识点
8.已知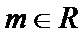
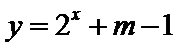
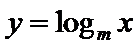
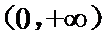
正确答案
解析
若函数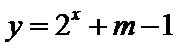
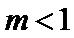
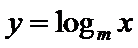
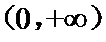
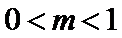
考查方向
解题思路
分别算出使得成立的m的取值范围。
易错点
充分和必要条件的判定出错。
知识点
10.已知



正确答案
解析
由函数





考查方向
解题思路
1、由选项找到解题方向——即

易错点
找不到解题的切入点。
知识点
16.定义在






正确答案
考查方向
易错点
1、函数

知识点
13.已知函数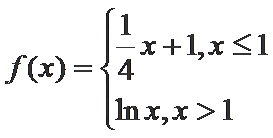
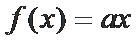
取值范围是___________
正确答案
解析
∵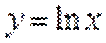
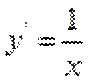
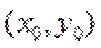
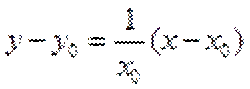
∴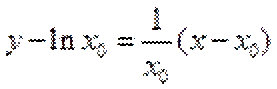
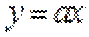
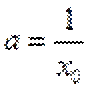
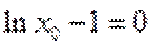
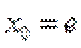
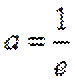
当直线与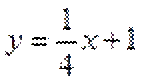
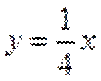
当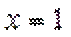
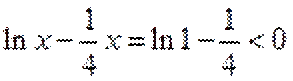
当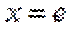
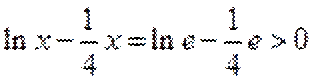
当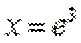
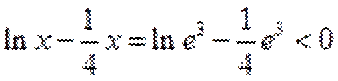
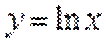
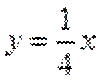
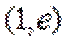
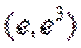
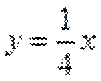
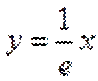
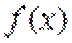
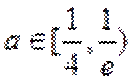
考查方向
解题思路
本题考查运用导数解决函数的能力,解题步骤如下: 先求导,找函数的切线方程,再利用零点的判定方法,找到a的取值范围。
易错点
本题必须注意审题,忽视则会出现错误。
知识点
扫码查看完整答案与解析