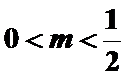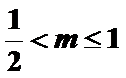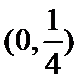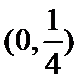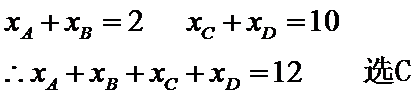- 函数与方程
- 共186题
10.已知函数





正确答案
解析









考查方向
解题思路
求出两个函数的零点,再去找到要求的最小值。
易错点
不知道怎么转化为所学知识来解答。
知识点
12.若函数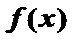


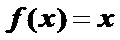
上,

正确答案
解析
当




考查方向
解题思路
根据已知定义域上的解析式求出未知的定义域上的解析式,在结合函数的图像找到要求解的范围。
易错点
本题不会由已知的解析式来求未知定义域上的解析式。
知识点
12.已知函数


①当
②函数
③
④
其中正确命题个数是( )
正确答案
解析
因为f(x)为R上的奇函数,设x>0,-x<0,则



当


同理判断4正确,所以选B
考查方向
解题思路
根据函数的相关性质,结合子题目,依次判断
易错点
求导错误;
知识点
22.(本题满分15分)设函数
(1)当

(2)已知函数
正确答案
(1) 

解析
试题分析:(1)利用函数解析式求出二次函数的对称轴,分类讨论求出函数的最小值;(2)设出方程
(1)当


当a≤﹣2时,函数f(x)在[﹣1,1]上递减,则
当﹣2<a≤2时,即有

当a>2时,函数f(x)在[﹣1,1]上递增,则
综上可得,
(2)设s,t是方程

由于0≤b-2a≤1,
由此
当0≤t≤1时,
由

得

当﹣1≤t<0时,
由


故b的取值范围是
考查方向
解题思路
(1)求出二次函数的对称轴方程,讨论对称轴和区间[﹣1,1]的关系,运用函数的单调性即可得到最小值;
(2)设s,t是方程
易错点
根据二次函数的对称轴求函数在闭区间上的单调性,基本不等式求最值时灵活变形.
知识点
12.如图,偶函数






正确答案
解析
由图象可知f(x)=0有三个根,0,
由图象可知,g(x)所对的每一个值都能有3个根,因此m=9,同理可得,n=9,所以选A.
考查方向
解题思路
结合函数图象把方程根的个数转化为函数图象的交点
个数,可分别求出m.n,进而得到答案
易错点
数型结合思想的相互转化错误
知识点
16.对于实数a,b,定义运算“⊗”:a⊗b=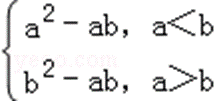
正确答案
解析
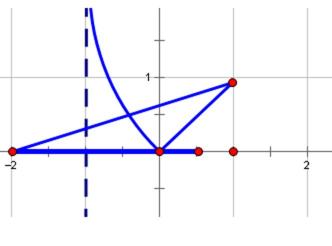
由题意可得函数的图像为下图,从图象上观察当关于X的方程为f(x)=m恰有三个互补相当的实数根时,函数的图形和直线y=m由三个不同的交点。再根据函数的极大值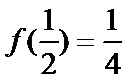
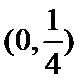
考查方向
解题思路
根据函数的解析式画出函数的图像,然后确定实数的取值范围。
易错点
计算错误,考虑情况不完全
知识点
10.已知定义在R上的奇函数y=f(x)
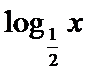
正确答案
解析
根据性质做出图像
共有4个零点ABCD,且AB关于x=1对称
CD关于x=5对称
考查方向
解题思路
1)根据函数性质得出函数在(0,6)上的图像,
2)数形结合得到零点
3)根据对称性得出零点间关系
易错点
主要易错于函数图像不能有效的画出
知识点
10.在区间[0,2]上任取两个实数a,b,则函数
正确答案
解析
在区间[0,2]上任取两个数a,b,对应的平面区域为边长为2的正方形,面积为4,要想使函数在区间内没有零点,则函数的最小值应该大于0,即


考查方向
解题思路
结合二次函数的性质求出函数在区间内没有零点的等价条件,利用几何概型的概率公式即可得到结论
易错点
数型结合思想掌握不好,几何概型理解不透彻
知识点
15.已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=

①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中真命题有
正确答案
①④
解析
对于①,因为f '(x)=2xln2>0恒成立,故①正确;
对于②,取a=-8,即g'(x)=2x-8,当x1,x2<4时n<0,②错误;
对于③,令f '(x)=g'(x),即2xln2=2x+a,记h(x)=2xln2-2x,则h'(x)=2x(ln2)2-2,存在












考查方向
解题思路
逐个判断各个选项的正误即可。
易错点
不明白题中给出的条件是什么;对于③④,不知道该如何判断正误。
知识点
15.若函数
正确答案
解析
∵当x=0时无零点,
考查方向
解题思路
1)对函数
2)当
3)讨论
4)借助单调性及其最值得出结论
易错点
本题易错在分类不清或者对单调性判断错误
知识点
扫码查看完整答案与解析