- 数列与函数的综合
- 共58题
1
题型:简答题
|
设等差数列{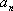
(1)求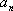
(2)设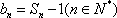
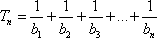
正确答案
见解析。
解析
知识点
数列与函数的综合
1
题型:
单选题
|
数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n≥1),则a6=( )
正确答案
A
解析
由an+1=3Sn⇒Sn+1-Sn=3Sn⇒Sn+1=4Sn,所以数列{Sn}是首项为1,公比为4的等比数列,所以Sn=4n-1,所以a6=S6-S5=45-44=3×44,所以选择A.
知识点
数列与函数的综合
1
题型:简答题
|
设数列







(1)求
(2)求数列
(3)记


正确答案
见解析。
解析
(1)当


所以
(2)当
所以
所以
由②-①得,
所以数列


所以
(3)当
当
所以
知识点
数列与函数的综合
1
题型:简答题
|
正项等比数列{an}的前n项和为Sn,a4 =16,且a2,a3的等差中项为S2。
(1)求数列{an}的通项公式;
(2)设
正确答案
见解析。
解析
知识点
数列与函数的综合
1
题型:
单选题
|
数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*),若b3=-2,b10=12,则a8=( )
正确答案
B
解析
由数列{bn}为等差数列,且b3=-2,b10=12可知数列公差d=2,所以通项bn=-2+(n-3)×2=2n-8=an+1-an,所以a8-a1=2×(1+2+3+…+7)-8×7=0,所以a8=a1=3.
知识点
数列与函数的综合
下一知识点 : 数列的极限
扫码查看完整答案与解析










