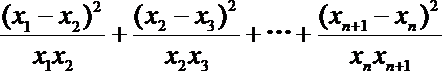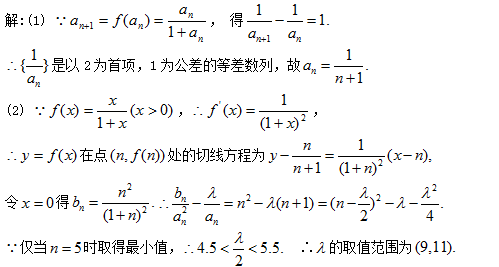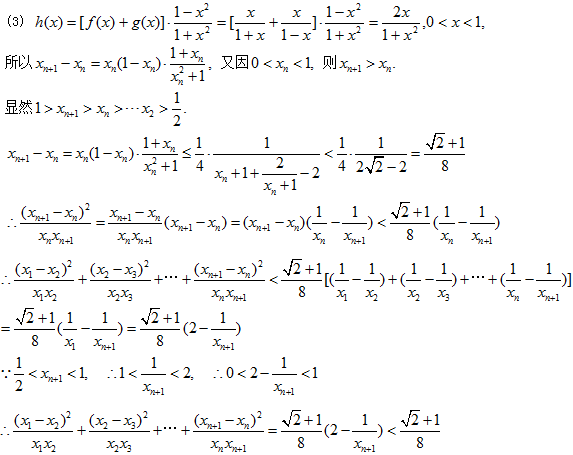- 数列与函数的综合
- 共58题
14.定义函数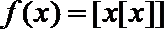
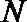
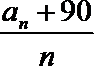
正确答案
13
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f-1(x)能确定数列{bn},bn=f-1(n).若对于任意n∈N*都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(Ⅰ) 设函数f(x)=
(Ⅱ)已知正数数列{cn}的前n项和
(Ⅲ)在(Ⅰ)和(Ⅱ)的条件下,d1=2,当n≥2时,设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 函数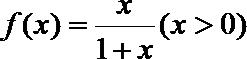
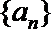
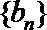
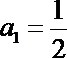
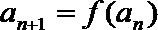
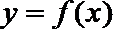
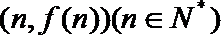
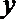
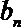
(1)求数列{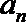
(2)若数列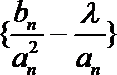
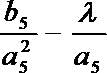
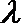
(3)若函数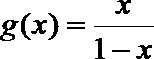
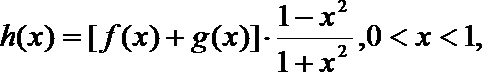
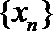
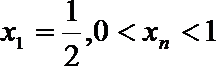
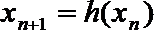
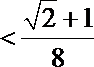
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(1)求函数
(2)若数列



(3)在(2)的条件下,证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设等差数列



(1)证明:数列
(2)若







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(1)求数列
(2)


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析