- 数列与函数的综合
- 共58题
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
对于无穷数列{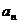
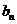
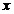
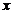
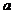


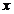
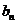
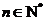
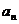
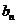
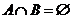
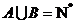
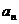
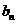
(1)若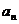
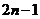
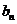
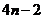
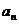
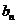
(2)若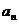
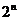
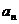
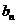
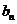
(3)若{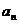
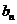
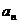
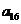
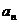
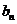
正确答案
(1)因为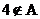
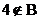

从而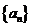
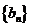
(2)因为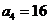
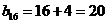
数列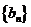
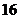
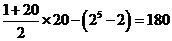
(3)设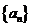
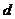
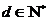
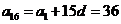
由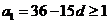
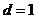
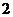
若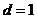
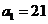
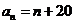
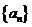
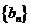
若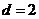
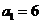
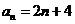
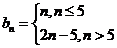
综上,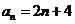
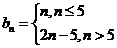
知识点
14.无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意的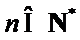
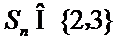
正确答案
解析
由于 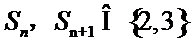
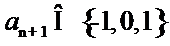
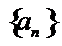
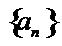
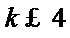
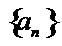
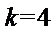
考查方向
解题思路
归纳,推理
易错点
推理的切入点
知识点
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
4.已知数列



正确答案
解析
因为











考查方向
解题思路
首先整理关系是





易错点
容易在指数运算、对数运算出错
知识点
4.已知数列



正确答案
解析
因为











考查方向
解题思路
首先整理关系是





易错点
容易在指数运算、对数运算出错
知识点
扫码查看完整答案与解析











