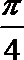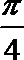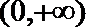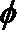· 函数的基本性质

· 复合函数的单调性

复合函数的单调性
共394题

· 函数的基本性质

· 复合函数的单调性

复合函数的单调性
共394题

热门试卷

X 查看更多试卷

1

题型：单选题

|

单选题 · 5 分

3．设函数，则满足的x的取值范围是( )

A，2]

B[0，2]

C[1，+)

D[0，+)

正确答案

D

解析

当x≤1时，21-x≤2的可变形为1-x≤1，x≥0，

∴0≤x≤1．当x＞1时，1-log2x≤2的可变形为x≥，

∴x≥1，

故答案为[0，+∞）．故选D．

知识点

复合函数的单调性

1

题型：单选题

|

单选题 · 5 分

8．函数的最小正周期为，为了得到函数的图象，只要将的图象（）.

A向左平移个单位长度

B向右平移个单位长度

C向左平移个单位长度

D向右平移个单位长度

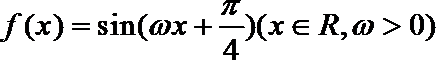
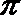
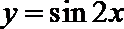
正确答案

A

解析

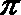
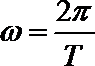
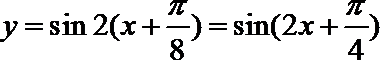
由T=,所以=2，因为，故选A.

知识点

复合函数的单调性

1

题型：简答题

|

简答题 · 14 分

21．已知函数，若

（1）求曲线在点处的切线方程；

（2）若函数在区间上有两个零点，求实数b的取值范围；

（3）当。

正确答案

（1）因为，

所以曲线在点处的切线方程为

（2）=，(x>0)

=，由>0得x>1, 由<0得0<x<1.

所以的单调递增区间是（1，+）,单调递减区间（0, 1）

x=1时，取得极小值.

因为函数在区间上有两个零点，

所以，解得，

所以b的取值范围是（1，

（3）当

即证：

即证：

构造函数：

当时，

所以，

又，所以

即

所以

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

1

题型：单选题

|

单选题 · 5 分

1．设集合（）

A

B（-1，0）

C（0，1）

D

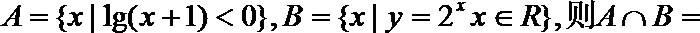
正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

1

题型：简答题

|

简答题 · 15 分

22．已知函数

（1）是否存在实数，使得在为增函数，为减函数，若存在，求出的值，若不存在，请说明理由；

（2）如果当时，都有恒成立，试求的取值范围。

正确答案

，，

（1）若，使在（0，）上递增，在（，）上递减，

则，

∴，这时，

当时，，递增。

当时，递减。

（2）

△＝

若△，即，则对恒成立，这时在上递减，∴。

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

继续学习学习下一知识点

下一知识点 : 函数的最值及其几何意义

百度题库 > 高考 > 理科数学 > 复合函数的单调性

扫码查看完整答案与解析