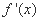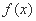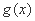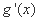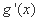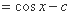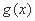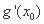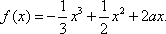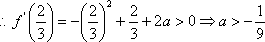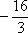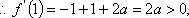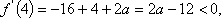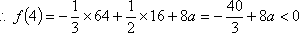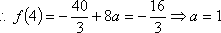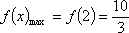- 函数的最值及其几何意义
- 共151题
若变量


正确答案
解析
【解析1】
画出可行域,由图可知,当直线




知识点
已知函数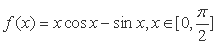
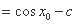
(1)求证: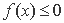
(2)若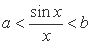
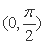
正确答案
见解析。
解析
(1)由

因为在区间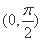
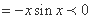
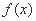
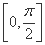
从而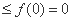
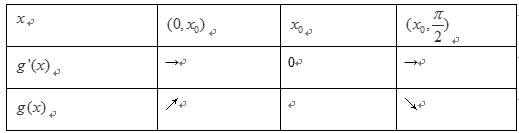
(2)当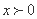
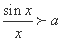
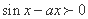
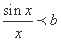
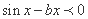
令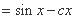
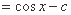
当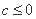
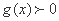
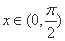
当
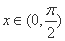
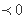
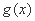
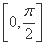
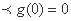
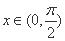
当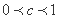
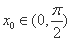
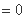
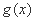
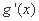
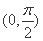
因为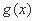
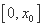
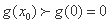

任意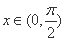
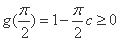
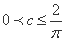
综上所述,当且仅当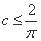
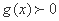
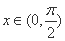
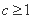
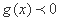
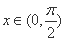
所以,若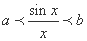
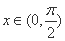

知识点
设
(1)若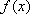
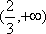

(2)当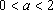
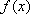
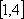
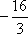
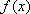
正确答案
见解析
解析
(1)已知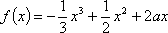
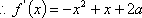
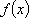
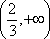
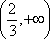
(2)已知0<a<2, 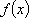
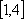

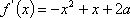
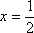
则必有一点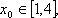
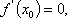
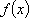
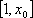
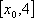
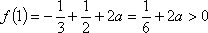
此时,由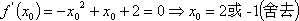
知识点
已知函数

(1)求
(2)求


正确答案
见解析。
解析
知识点
有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若




正确答案
解析
假设AB两个同学的数学成绩一样,由题意知他们语文成绩不一样,这样他们的语文成绩总有人比另一个人高,语文成绩较高的同学比另一个同学“成绩好”,与已知条件“他们之中没有一个比另一个成绩好”相矛盾.因此,没有任意两个同学数学成绩是相同的.因为数学成绩只有3种,因而同学数量最大为3.即 3位同学成绩分别为(优秀,不合格)、(合格,合格)、(不合格,优秀)时满足条件.
知识点
扫码查看完整答案与解析