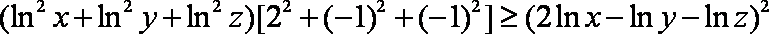- 复合函数的单调性
- 共394题
已知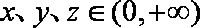
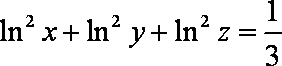
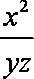
正确答案
解析
知识点
设函数
(1)若对定义域内的任意


(2)若函数
(3)若


正确答案
见解析
解析
(1)由



因为对

故有
又

经检验,当




故满足
(2)



即

若



因为



综上所述,实数b的取值范围是
(3)当

令
则
当

所以函数

又


即
故当



则有

知识点
已知




正确答案
见解析。
解析
因为

当且仅当

所以
知识点
对于实数






①

(1)若

(2)当



正确答案
(1)

解析
(1)若


(2)当





①当



②当



综上,
知识点
已知矩阵A=
(1)求a,b的值;
(2)求属于λ2的一个特征向量
正确答案
见解析。
解析
(1)令f(λ)=
于是λ1+λ2=a+4,λ1λ2=4a+b,解得a=1,b=2
(2)设






故


知识点
某工厂有216名工人,现接受了生产1000台GH型高科技产品的总任务。
已知每台GH型产品由4个G型装置和3 个H型装置配套组成,每个工人每小时能加工6个G型装置或3 个H型装置,现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组)设加工G型装置的工人有x人,他们加工完成G型装置所需的时间为g(x),其余工人加工完成H型装置所需的时间为h(x)(单位:小时,可不为整数)。
(1)写出g(x),h(x)的解析式;(2)写出这216名工人完成总任务的时间f(x)的解析式;(3)应怎样分组,才能使完成总任务用的时间最少?
正确答案
(1)
(2)
(3)加工G型装置,H型装置的人数分别为86、130或87、129
解析
解析:(1)由题意知,需加工G型装置4000个,加工H型装置3000个,所用工人分别为



即



(2)
∵0<x<216,∴216-x>0,
当



当





(3)完成总任务所用时间最少即求
当


∴


当


∴

∴
∴加工G型装置,H型装置的人数分别为86、130或87、129。 ………12分
知识点
已知函数





(1)求函数
(2)若函数在开区间

(3)设函数


正确答案
见解析
解析
(1)设
则可设

因为
所以

由

所以
(2)由(1)得
由题意得,三次函数在开区间上存在的最大值与最小值必为极值(如图),
又



解得
(3)题设等价与

所以a,b,c均小于
假设在a,b,c中有两个不等,不妨设a


若a



又由

于是a


同理,若a
故假设不成立,所以
知识点
如图,AB是半圆的直径,C是AB延长线上一点,CD切
半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的
中点,求BC的长。
正确答案
见解析
解析
解:连接OD,则OD⊥DC,
在Rt△OED中,

所以∠ODE
在Rt△ODC中,∠DCO



所以BC
知识点
在平面直角坐标系xOy中,已知点




正确答案
见解析
解析
由




将点


知识点
(1)计算:C

(2)观察下面一组组合数等式:C





正确答案
见解析。
解析
(1)原式=C

(2)由C

2C

3C

…
可得第k(k∈N*)个等式为:
kC

证明如下:kC



知识点
扫码查看完整答案与解析