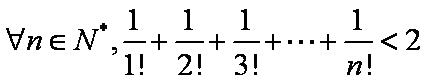- 复合函数的单调性
- 共394题
某种平面分形图如下图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为 120°;二级分形图是在一级分形图的每一条线段末端出发再生成 两条长度均为原来


则(1)
(2)
正确答案
(1)
解析
依题意,(1)记




(2)
知识点
已知函数

正确答案
解析
解析:(1)




所以函数

知识点
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是
(1)求油罐被引爆的概率。
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望
正确答案
见解析。
解析
(1)“油罐被引爆”的事件为事件A,其对立事件为

∴P(A)=1-
(2)射击次数ξ的可能取值为2,3,4,5,
P(ξ=2)=

P(ξ=4)=C
故ξ的分布列为:
Eξ=2×



知识点
在直角坐标系中,已知△ABC的顶点坐标为A(0,0)、B(1,1)、C(0,2),求△ABC在矩阵MN作用下变换所得到的图形的面积
这里M=


正确答案
见解析。
解析
在矩阵N=





△ABC在矩阵MN作用下变换所得到的图形与△ABC全等,从而其面积等于△ABC的面积,即为1
知识点
已知圆C的参数方程为
正确答案
见解析。
解析
圆C的参数方程为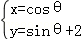
所以圆C的方程为 x2+(y﹣2)2=1;圆的圆心坐标(0,2),半径为1,
直线l的极坐标方程为ρsinθ+ρcosθ=1,
所以直线l的方程为 x+y=1。
圆心到直线的距离为:
圆心到直线的距离,半径,半弦长满足勾股定理,
故所求弦长为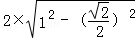
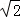
知识点
已知函数

(1)求
(2)设不等式



(3)设

正确答案
见解析
解析
(1)因为

令





所以函数


所以当


(2)因为不等式


所以对任意

由

当

将



当



所以


所以当


故实数

(3)由(1)知,对任意实数


令


所以
即
所以
因为
所以 
知识点
证明:
正确答案
见解析。
解析
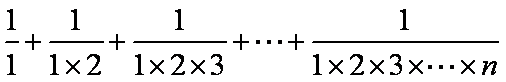

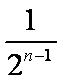
知识点
(1)求函数
(2)已知函数
正确答案
(1)
解析
解析:(1)
令





∴当


当


(2)令


又


∴a≥2. ……………………………(12分)
知识点
在直角坐标系中,曲线C的参数方程为



(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与直线C的两个交点为A、B,求
正确答案
见解析
解析
(1)直线
直线



(2)直线


将直线
有
设两根为

知识点
如图所示,四棱锥








(1)求证:平面

(2)求直线

(3)求点

正确答案
见解析
解析
解析:(1)设





则



又∵

又∵

∴
又∵




∵



(2)连结



则由(1)知平面

且
得





在

在


即直线


(3)由于








从而点


知识点
扫码查看完整答案与解析