- 空间图形的公理
- 共46题
如图,在三棱柱



(1)求证:

(2)求证:直线

(3)设




正确答案
见解析
解析
(1)证明:因为三棱柱的侧面是正方形,
所以

所以

因为


由已知可得,底面
因为


因为


(2)证明:如图,连接



显然点

因为


又因为



所以直线

(3)在


此时点

过



由(1)可知



所以
又



又


知识点
设m、n是两条不同的直线,
正确答案
解析
举反例否定A、B、C
排除A、B、C
或直接据D推断
知识点
如图,在直三棱柱ABC-


(1)求证:
(2)当三棱锥


正确答案
见解析
解析
解析:(1)证明:连

又

另证:建立空间直角坐标系,证明
(2)设AE=
当且仅当
取





在
根据余弦定理得
知识点
如图,在底面为直角梯形的四棱锥P-ABCD中AD∥BC,∠ABC=90°PD⊥平面ABCD,AD=1,AB=
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成的角;
(3)在线段PC上是否存在一点E,使得DE∥平面PAB?若存在,确定点E的位置;若不存在,请说明理由。
正确答案
见解析
解析
(1)证明:在直角△ABD中,AD=1,AB=
∴∠ABD=30°
∴∠DBC=60°
在△DBC中,CD2=BD2+BC2-2BD×BC×cos60°=4+16-2×2×4×
∴BC2=CD2+BD2,
∴BD⊥CD
∵PD⊥平面ABCD,BD⊂平面ABCD
∴PD⊥BD
∵PD∩CD=D
∴BD⊥平面PCD
∵PC⊂平面PCD
∴BD⊥PC;
(2)解:∵PD⊥平面ABCD,PD⊂平面ABCD。
∴平面PDC⊥平面ABCD。
过D作DF∥AB交BC于F,过点F作FG⊥CD交CD于G,则∠FDG为直线AB与平面PDC所成的角。
在Rt△DFC中,∠DFC=90°,DF=
∴tan∠FDG=
即直线AB与平面PDC所成角为60°。
(3)解:存在,且满足
连接EF,∵DF∥AB,∴DF∥平面PAB。
又∵DE∥平面PAB,DE∩DF=D
∴平面DEF∥平面PAB,
∵EF⊂平面DEF,∴EF∥AB。
又∵AD=1,BC=4,BF=1
∴
知识点
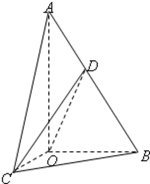
如图,在Rt△AOB中,∠OAB= 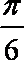
(1)求证:平面COD⊥平面AOB;
(2)求异面直线AO与CD所成角的大小。
(3)求CD与平面所AOB所成角的最大值.
正确答案
见解析
解析
(1)∵Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到
∴CO⊥AO,BO⊥AO
又∵二面角B-AO-C是直二面角
∴∠BOC是二面角B-AO-C的平面角
∴∠BOC=90°
∴CO⊥BO,又AO∩BO=O
∴CO⊥平面AOB
∵CO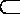
∴平面COD⊥平面AOB
(2)作DE⊥OB,垂足为E,连接CE,所以DE∥AO
∴∠CDE是异面直线AO与CD所成的角。
在 Rt△COE中,CO=BO=2,OE=
∴CE=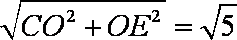

∴CD=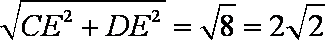
cos∠CDE=
∴异面直线AO与CD所成角为arcos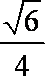
(3)由(I)知,CO⊥平面AOB(这是保证),∴∠CDO是CD与平面AOB所成的角,且tan∠CDO=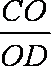
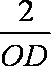
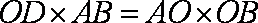
,tanCDO=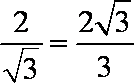
∴CD与平面AOB所成最大角的正切值为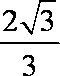
知识点
扫码查看完整答案与解析