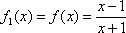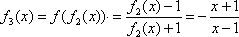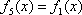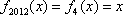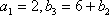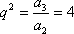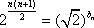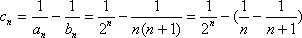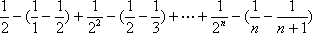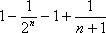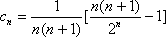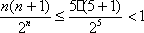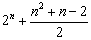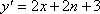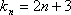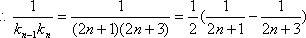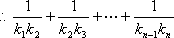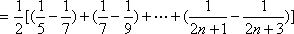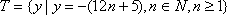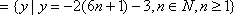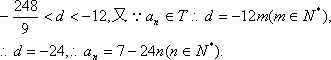- 数列求和、数列的综合应用
- 共491题
设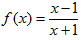
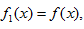
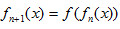
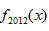
正确答案
x
解析
由题目可预知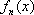
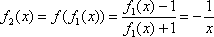
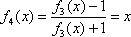
……,可知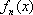
知识点
已知数列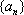
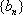
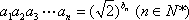
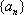
(1) 求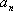
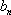
(2) 设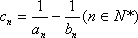


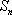
(i)求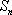
(ii)求正整数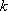
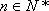
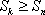
正确答案
见解析
解析
(1)∵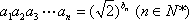
当n≥2,n∈N*时,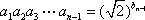
由①②知:当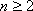
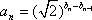
∵b3=6+b2, ∴a3=8。
∵{an}为等比数列,且a1=2,∴{an}的公比为q,则
由题意知an>0,∴q>0,∴q=2。
∴an=2n(n∈N*)。
又由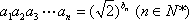
即
∴bn=n(n+1)(n∈N*)。
(2)(i)∵
∴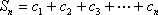
=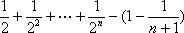
=
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
而
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有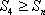
知识点
已知数列


(1)求
(2)求

(3)记数列




正确答案
(1)3,13,39(2)
解析
(1)


(2)由题知,有

∴
(3) ∵
∴
∴
又






综上,有
知识点
已知数列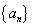

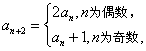

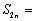
正确答案
7;
解析
略
知识点
14.数列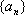
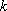
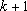
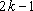
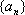
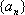


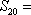

正确答案
36;3983
解析
略
知识点
已知数列







(1)判断数列

(2)求
正确答案
见解析。
解析
(1)




所以




(2)由(1)可知







知识点
已知集合







(1)当




(2)(ⅰ)证明:若



(ⅱ)设



说明理由;
(3)记




正确答案
见解析
解析
(1)解:当

得 

由 


(2)(ⅰ)证明:设


因为 

所以 

即 


所以 

所以

(ⅱ)解:设



反例如下:取


则 



因为

所以不存在

(3)解法一:因为 
设






所以
因为 
所以 

所以 
因为

又 
所以

即 
对于 





综上,

解法二:首先证明如下引理:设

证明:因为 

所以 
即 
所以

上式等号成立的条件为


对于 





综上,

知识点
定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x。则f(1)+f(2)+f(3)+…+f(2012)=
正确答案
解析


知识点
在公差为



(1)求
(2)若
正确答案
(1)
(2)
解析
(1)由已知得到:


(2)由(1)知,当

①当
②当
所以,综上所述:
知识点
在直角坐标平面上有一点列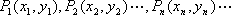

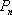
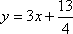
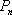
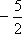
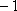
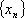
(1)求点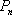
(2)设抛物线列


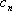
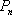
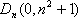
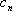
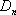
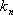
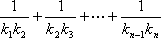
(3)设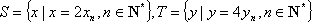
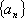
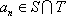
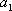
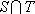
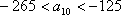
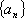
正确答案
见解析
解析
(1)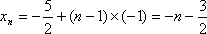
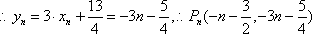
(2)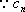

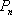

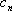
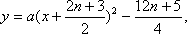
把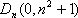
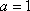
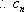
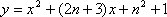
当
=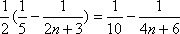
(3)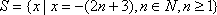
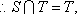
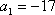
设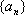
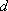
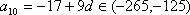
············································13分
知识点
扫码查看完整答案与解析