• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 数列求和、数列的综合应用
  • 共491题
  • 数列求和、数列的综合应用
  • 共491题

热门试卷

X 查看更多试卷
1
题型：简答题
|
简答题 · 12 分

21.设.

（1）求实数a；

（2）求数列{xn}的通项公式；

（3）若，求证：b1+b2+…+bn<n＋1。

正确答案

（1）由

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式裂项相消法求和数列与函数的综合数列与不等式的综合
1
题型：简答题
|
简答题 · 12 分

16． 设等差数列{an}的前n项和为Sn，且S4＝4S2，a2n＝2an＋1．

（Ⅰ）求数列{an}的通项公式；

（Ⅱ）证明：对一切正整数n，有．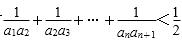

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等差数列的基本运算等差数列的性质及应用裂项相消法求和数列与不等式的综合
1
题型： 单选题
|
单选题 · 5 分

8．已知数列{an}的各项均为正数，前n项和为Sn，且，n∈N*，则数列的前100项和为 (　  　)

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an裂项相消法求和
1
题型：简答题
|
简答题 · 12 分

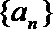
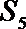
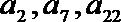
18．已知等差数列的公差不为零，其前n项和为，若=70，且成等比数列

（Ⅰ）求数列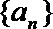的通项公式；

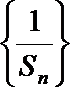
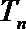
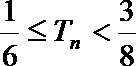
（Ⅱ）设数列的前n项和为，求证：。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项裂项相消法求和数列与不等式的综合等差数列与等比数列的综合
1
题型： 单选题
|
单选题 · 5 分

7．数列1，，，……，的前n项和为（    ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式裂项相消法求和
1
题型：填空题
|
填空题 · 5 分

8.在数列{an}中，a1＝6，且对任意大于1的正整数n，点（，）在直线x－y＝上，则数列{}的前n项和Sn＝_________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式裂项相消法求和
1
题型：填空题
|
填空题 · 5 分

10．若数列中，，其前n项的和是，则在平面直角坐标系中，直线在y轴上的截距为__________。  

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

裂项相消法求和直线的截距式方程
1
题型：简答题
|
简答题 · 12 分

19．已知函数，数列满足条件：．

（1）求证：数列为等比数列；

（2）令是数列的前项和，求使成立的最小的值．

正确答案

（1）证明：由题意得，∴ 

又 ∵ 

∴ 

故数列{bn + 1}是以1为首项，2为公比的等比数列

（2） 由 （1）可知，，∴ 

故

∴ 

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的判断与证明裂项相消法求和数列与函数的综合数列与不等式的综合
1
题型：简答题
|
简答题 · 16 分

19. 设数列的前项和，，，且当时，．

（1）求证:数列是等比数列，并求数列的通项公式；

（2）令，记数列的前项和为．设是整数，问是否存在正整数，使等式成立？若存在，求出和相应的值；若不存在，说明理由．

正确答案

见解析

解析

解：（1）当时, ,,

代入并化简得,

而恒为正值,∴

∴数列是等比数列.

∴.当时,,

又，∴

（2）当时，,此时 ，又

∴.

故，

当时，

，

若，

则等式为，不是整数，不符合题意；

若，则等式为，

∵是整数,   ∴必是的因数,  ∵时

∴当且仅当时，是整数，从而是整数符合题意.

综上可知，当时，存在正整数，使等式成立，

当时，不存在正整数使等式成立.

考查方向

本题考查了等比数列的证明及数列的通项公式求法

解题思路

利用，得数列是等比数列.

易错点

忽略n的范围的讨论。

知识点

由an与Sn的关系求通项an等比数列的判断与证明裂项相消法求和数列与函数的综合
1
题型：简答题
|
简答题 · 12 分

17. 在等差数列中，，数列的前n项和.

（Ⅰ）求数列，的通项公式;

（Ⅱ）求数列的前n项和．

正确答案

见解析

解析

（Ⅰ）设等差数列的首项为，公差为d，则

   

数列的前n项和

当n=1时，，

当n2时，，对=4不成立，

所以，数列的通项公式为

（Ⅱ）n=1时，，

n2时， ，

所以

n=1仍然适合上式，

综上，

考查方向

等比数列，等比数列的前n项和

解题思路

利用构造的等比数列求前n项和公式的求解

易错点

构造等比数列

知识点

由递推关系式求数列的通项公式等差数列的基本运算裂项相消法求和
继续学习 棒棒哒，已是最后一个知识点
已完结
百度题库 > 高考 > 理科数学 > 数列求和、数列的综合应用

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题