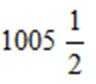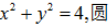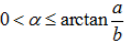数列求和、数列的综合应用
共491题

数列求和、数列的综合应用
共491题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 12 分

17.已知数列的前n项和，，其中0

（I）证明是等比数列，并求其通项公式

（II）若，求

正确答案

知识点

其它方法求和

题型：简答题

简答题 · 12 分

17.本小题满分12分）

为等差数列的前n项和，且记，其中表示不超过x的最大整数，如.

（I）求；

（II）求数列的前1 000项和.

正确答案

知识点

等差数列的性质及应用等差数列的前n项和及其最值其它方法求和

题型：简答题

简答题 · 12 分

18.（本小题满分12分）

已知数列的前n项和Sn=3n2+8n，是等差数列，且

（Ⅰ）求数列的通项公式；

（Ⅱ）另求数列的前n项和Tn.

正确答案

知识点

等差数列的性质及应用其它方法求和等差数列与等比数列的综合

题型：填空题

填空题 · 12 分

本小题满分12分）

为等差数列的前n项和，且记，其中表示不超过x的最大整数，如.

（I）求；

（II）求数列的前1 000项和.

正确答案

试题解析：（Ⅰ）设的公差为，据已知有，解得

所以的通项公式为

（Ⅱ）因为

所以数列的前项和为

知识点

等差数列的性质及应用其它方法求和

题型：简答题

简答题 · 15 分

已知正项数列的前项和满足：，（）.

20. 求；

21. 若，求数列的前项和.

第(1)小题正确答案及相关解析

正确答案

1．

解析

试题分析：本题属于数列知识的综合应用问题，属于简单题，只要掌握相关的知识，即可解决本题，解析如下：因为，

所以当时，，两式相减得，，化简得，，由于是正项数列，所以，

所以，即对任意都有，又由得，，解得或（舍去），所以是首项为3，公差为2的等差数列，

所以.

考查方向

本题考查了数列的通项公式、数列求和等知识点。

解题思路

直接利用的关系即可求出通项公式；

易错点

正确答案

．

解析

试题分析：本题属于数列知识的综合应用问题，属于简单题，只要掌握相关的知识，即可解决本题，解析如下：由已知及（Ⅰ）知，，， ①

， ②

②-①得，

考查方向

本题考查了数列的通项公式、数列求和等知识点。

解题思路

先求出，再利用错位相减法求和．

易错点

正确答案

-2

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质导数的几何意义其它方法求和

题型：填空题

填空题 · 5 分

15．已知函数，正项等比数列满足，则等于（）．

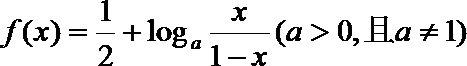
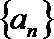
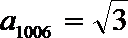
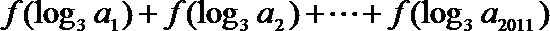
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质等比数列的基本运算其它方法求和

题型：简答题

简答题 · 18 分

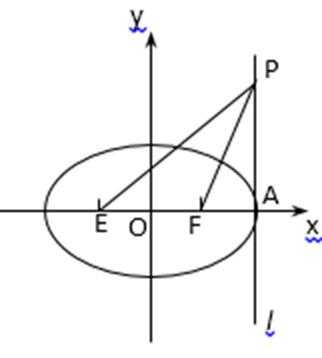
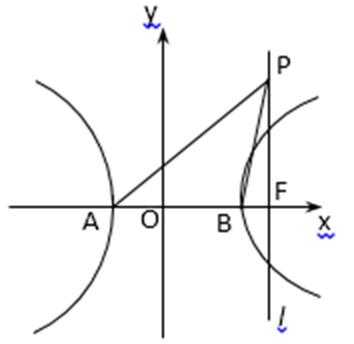
22．（1）A（–2，0）、B（2，0），M满足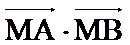=0．求M轨迹；

（2）若（1）中的轨迹按向量（1，–1）平移后恰与x+ky–3=0相切，求k．

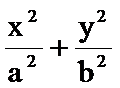
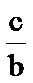
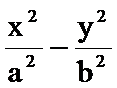
（3）如图，l过=1 （a>b>0）长轴顶点A且与长轴垂直的直线，E、F是两焦点，P∈l，P、A不重合，若∠EPF=α，则有0<αarctan，类比此结论到=1 （a>0，b>0），l是过焦点F且垂直x轴的直线，A、B是两顶点，P∈l，P、F不重合，∠APB=α，求α取值范围．

正确答案

（1）

（2）

（3）

解析

解析已在路上飞奔，马上就到！

知识点

其它方法求和

题型：填空题

填空题 · 5 分

14.已知数列与的前项和分别是和，已知，记，那么数列的前100项和（）

正确答案

2009

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式其它方法求和分析法的思考过程、特点及应用

题型：单选题

单选题 · 5 分

5.已知数列{an}满足a1=33,an+1-an=2n,则的最小值为（　　　）

正确答案

解析

因为an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2[(n-1)+(n-2)+…+1]+33=33+n2-n,

所以

设

令,得 ,

则f(x)在上单调递减,在上单调递增,

故当时函数有最小值,而n为正整数,经验证,n=6时满足题意,此时的最小值为

知识点

其它方法求和

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 数列求和、数列的综合应用

扫码查看完整答案与解析