- 数列求和、数列的综合应用
- 共491题
17.在数列



(I)求数列
(II)求数列


(III)证明存在




正确答案
(I)解法一:


由此可猜想出数列

以下用数学归纳法证明.
(1)当

(2)假设当
那么,
这就是说,当
根据(1)和(2)可知,
等式


解法二:由
可得
所以
故
所以数列
(II)
设

当
这时数列

当



(III)通过分析,推测数列

下面证明:
由


所以③式成立.
因此,存在



解析
解析已在路上飞奔,马上就到!
知识点
23.一青蛙从点





(1)若点





(2)若点




(3)若点




正确答案
(1)设
所以

(2) 依题意,
随着

(方法二)∴



又
∴
于是,当
当
∴
解析
解析已在路上飞奔,马上就到!
知识点
21. 









(1)求函数
(2)设

(3)若(2)中数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列

(1) 求证:数列

(2) 求数列


(3) 若数列





正确答案
(1)∵
∴数列

数列


(2)
(3)


所以

∴
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知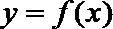
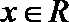
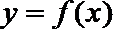
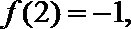
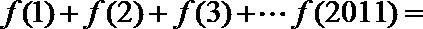
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于集合N={1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对n=3、n=4的情况,计算它的“交替和”的总和S3、S4,并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和Sn= _______。
正确答案
n∙2n–1
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{




(1)求数列{

(2)若数列{



(3)在(2)的条件下,数列{
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列 的前n项和Sn=10n-n2(n∈N+),则数列 的前n项和Tn为 .
正确答案
解析
当n=1时,a1=S1=9;当n≥2时,an=Sn-Sn-1=11-2n,
由于n=1时,a1=9也满足11-2n,
因此an=11-2n.
(1)当n>5时,
(2)当n≤5时,
综合(1)(2),得
知识点
11.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.对于一个有限数列p=(p1,p2,…,pn),p的“迤俪森”定义为
正确答案
解析
由“迤俪森”定义,得(p1,p2,…,p99)的“迤俪森”和为

知识点
扫码查看完整答案与解析






















































