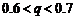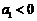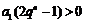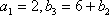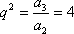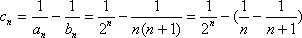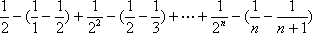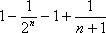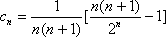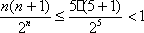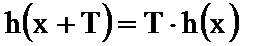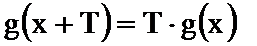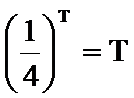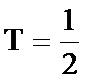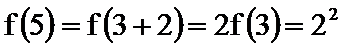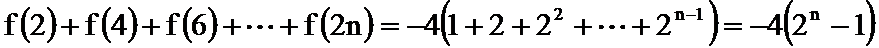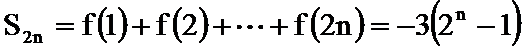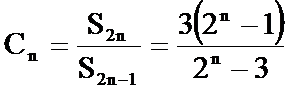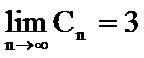- 数列求和、数列的综合应用
- 共491题
11. 无穷数列
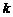
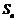
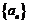
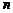
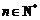
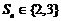
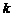
值为___________
正确答案
知识点
17. 已知无穷等比数列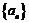
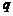
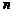
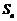
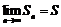
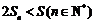
正确答案
解析
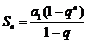
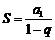
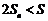
若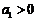
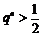
若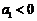
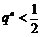
知识点
已知


27.设



28.设






29.设





正确答案
(1)
解析
(1)因为

所以
进而
由已知可知

考查方向
解题思路
根据函数的单调性求出

易错点
1.错将能成立问题转化为恒成立问题处理;2.对于题中出现的字母太多导致无法入手。
正确答案
(2)略;
解析
(2)当

所以
进而


由于区间

所以

因此,
考查方向
解题思路
先根据题意确定
易错点
1.错将能成立问题转化为恒成立问题处理;2.对于题中出现的字母太多导致无法入手。
正确答案

解析
(3)由于
所以

进而
由题意对任意

当


当


综上,实数

考查方向
解题思路
先求出
易错点
1.错将能成立问题转化为恒成立问题处理;2.对于题中出现的字母太多导致无法入手。
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数fn(x)=
(1)对每个n∈N*,存在唯一的xn∈
(2)对任意p∈N*,由(1)中xn构成的数列{xn}满足0<xn-xn+p<.
正确答案
见解析
解析
(1)对每个n∈N*,当x>0时,f′n(x)=
由于f1(1)=0,当n≥2时,fn(1)=
又

所以存在唯一的xn∈
(2)当x>0时,fn+1(x)=fn(x)+
由fn+1(x)在(0,+∞)内单调递增知,xn+1<xn,故{xn}为单调递减数列,
从而对任意n,p∈N*,xn+p<xn.
对任意p∈N*,
由于fn(xn)=
fn+p(xn+p)=
①式减去②式并移项,利用0<xn+p<xn≤1,
得xn-xn+p=

因此,对任意p∈N*,都有0<xn-xn+p<
知识点
已知数列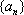
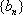
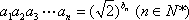
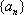
(1) 求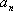
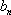
(2) 设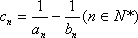


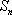
(i)求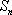
(ii)求正整数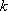
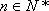
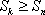
正确答案
见解析
解析
(1)∵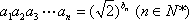
当n≥2,n∈N*时,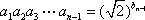
由①②知:当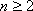
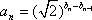
∵b3=6+b2, ∴a3=8。
∵{an}为等比数列,且a1=2,∴{an}的公比为q,则
由题意知an>0,∴q>0,∴q=2。
∴an=2n(n∈N*)。
又由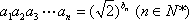
即
∴bn=n(n+1)(n∈N*)。
(2)(i)∵
∴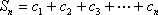
=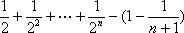
=
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
而
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有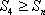
知识点
设数列





(1)求
(2) 求数列
(3) 证明:对一切正整数

正确答案
见解析
解析
(1)因为



当


联立上述三个式子可得
(2)由(1)可知
当



即


所以


所以

(3) 当



当
又因为

所以
知识点
数列
正确答案
:
解析
利用等比数列求和公式


考查方向
本题主要考查了等比数列求和的基本运算
易错点
等比数列的求和公式忘记
知识点
5.无穷等比数列



则前


正确答案
解析
第一步,先求出等比数列


第二步,因为


考查方向
解题思路
本题应该分为两步,首先求出等比数列



易错点
本题必须注意
(1)只有公比


(2)只有公比



知识点
23.已知函数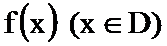
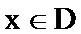
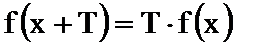
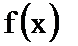
(1)判断
(2)证明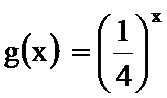
(3)若
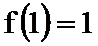
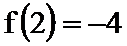
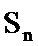
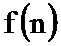
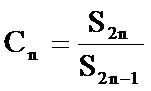
正确答案
(1)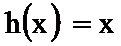
(2)证明略
(3)
解析
解:(1) 设:
则 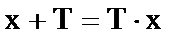
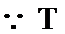
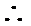
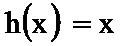
(2) 设:
则 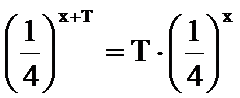
下证唯一性:
若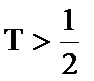
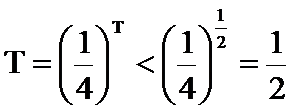
若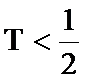
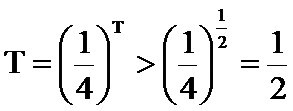
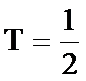
(3)
同理:
同理:
考查方向
解题思路
首先作到最后,要有耐心和信心,认真审题,发掘题目中的可利用信息。第一问直接证明有困难,可以考虑反证法;第三问因为奇数项和偶数项的变化规律不同,宜采用分组求和法。
易错点
第三问数列的奇数项和偶数项要区别对待,忽视容易产生错误。
知识点
扫码查看完整答案与解析