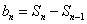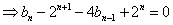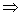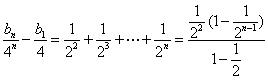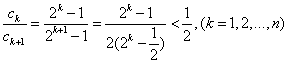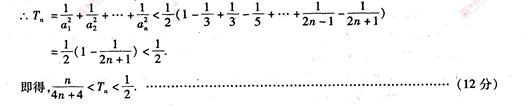- 数列求和、数列的综合应用
- 共491题
数列






(1)若数列





(2)证明:一个等比数列为


(3)若











正确答案
见解析
解析
(1)由




于是
所有满足条件的数列





(2)(必要性)设数列









所以


(充分性)若一个等比数列



以

若一个等比数列





(3)因



所以数列

假设存在正整数

切
当



下面证明:

由于
所以
知识点
已知等比数列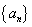
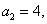
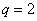
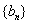
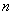
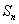
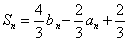

(1)求数列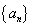
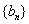
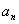
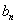
(2)设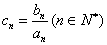
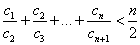
正确答案
见解析。
解析
(1) 解法一:由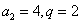
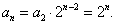
由上式结合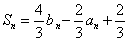
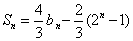
则当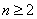
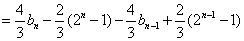
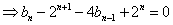
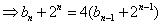
∵
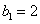
∴数列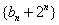
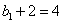
∴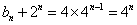
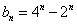
【解法二:由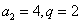
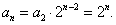
由上式结合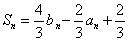
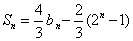
则当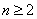
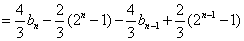
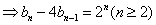
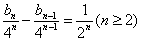
∴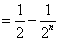
∵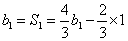
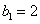
∴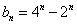
(2) 由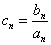
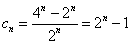
【或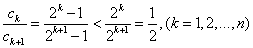
∴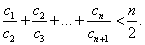
知识点
设等比数列




(1)求数列
(2)在




求证:

正确答案
见解析。
解析
(1)设等比数列






即

当


即
(2)①

设

① -②得:
=
知识点
已知数列



(1)求

(2)求
(3)设




正确答案
见解析。
解析
(1)当


当


(2)(法一)当


①—②得:





另解:
又



(法二)根据


用数学归纳法证明如下:
(1)当

(2)假设当

那么当

即:
又 
①-②得:
解,得


因此,由数学归纳法证得
(3)


知识点
设数

(1)求证:数列
(2)若

正确答案
见解析。
解析
(1)
(2)
知识点
请阅读下列材料:若两个正实数a1,a2满足

证明:构造函数




根据上述证明方法,若n个正实数满足
正确答案
解析
略
知识点
已知正项数列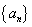
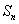
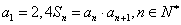
(1)求数列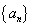
(2)设数列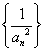

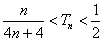
正确答案
见解析。
解析
知识点
已知正项数列



(1)求数列
(2)设






正确答案
见解析。
解析
(1)法一:由
当


当



∵正项数列
∴
∴


∴ 
∴ 
法二:
当


由

当
∴ 
整理得
∵正项数列

∴ 
∴


∴ 
(2)证明:先证:
.
故只需证
因为[
所以
所以
当


相加得:
即:
知识点
设函数



(1)求函数
(2)当

(3)设



正确答案
见解析。
解析
(1)显然


令
ⅰ)当




ⅱ)当




在区间



(2)ⅰ)


ⅱ)

于是:

由(1)可知

即证明不等式

(法一)由上可知:不等式

若

故
即当


故当


(法二)令



由表


即

由于

故函数

又当

于是指数函数

同理当

于是指数函数

于是,当

从而函数



易知当


当


又易知

综上,当



(3)证法一:令


则不等式
注意到:




于是

故
从而


故原不等式
证法二:同上可将不等式

即



又
故
于是

又

知识点
已知数列{




(1)求

(2)设



正确答案
见解析。
解析
知识点
扫码查看完整答案与解析