数列求和、数列的综合应用_章节学习

1

题型：单选题

|

单选题 · 5 分

10.已知数列(n∈N*)满足且t<a1<t+1,其中t>2,若则实数k的最小值为(　　).

A2

B3

C4

D5

正确答案

C

解析

由于t<a1<t+1,

得a2=a1-t,

易得0<a1-t<1,

即0<a2<1,又t>2,

那么a3=t+2-a2=2t+2-a1,

又t+1<2t+2-a1<t+2,

即

又1<t+2-a1<2,

即1<a4<2,

得a4<t,

从而a5=t+2-a4=a1,

结合

可得实数k的最小值为4.

知识点

由递推关系式求数列的通项公式数列与不等式的综合

1

题型：简答题

|

简答题 · 13 分

19.已知数列{bn}的前n项和．数列{an}满足，数列{cn}满足．

（1）求数列{an}和数列{bn}的通项公式；

（2）若对一切正整数n恒成立，求实数m的取值范围．

正确答案

（1）当时，

又适合上式

∴

由

（2）

∵

∴ ，即

∴ {cn}的最大项为

∴

∴ 实数m的取值范围为

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式错位相减法求和数列与不等式的综合

1

题型：单选题

|

单选题 · 5 分

10.已知数列 (n∈N*)满足且t<a1<t+1,其中t>2,若则实数k的最小值为(　　).

A2

B3

C4

D5

正确答案

C

解析

由于t<a1<t+1,

得a2=a1-t,

易得0<a1-t<1,

即0<a2<1,又t>2,

那么a3=t+2-a2=2t+2-a1,

又t+1<2t+2-a1<t+2,

即

又1<t+2-a1<2,

即1<a4<2,

得a4<t,

从而a5=t+2-a4=a1,

结合

可得实数k的最小值为4.

知识点

由递推关系式求数列的通项公式数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

19．已知函数，数列满足条件：．

（1）求证：数列为等比数列；

（2）令是数列的前项和，求使成立的最小的值．

正确答案

（1）证明：由题意得，∴

又 ∵

∴

故数列{bn + 1}是以1为首项，2为公比的等比数列

（2）由（1）可知，，∴

故

∴

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的判断与证明裂项相消法求和数列与函数的综合数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

21.已知数列的首项

（1）求的通项公式；

（2）证明：对任意的．

正确答案

（1）

∴ ∴

又 ∵

∴ 是以为首项，为公比的等比数列

∴

（2）由 (1) 知

∴ 原不等式成立

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等比数列的基本运算等比数列的判断与证明数列与不等式的综合

1

题型：简答题

|

简答题 · 16 分

22.给定数列，记该数列前项中的最大项为，即；该数列后项中的最小项为，即；．

（1）对于数列：3,4,7,1，求出相应的；

（2）若是数列的前项和，且对任意有其中为实数，且．

①设，证明数列是等比数列；

②若数列对应的满足对任意的正整数恒成立，求实数的取值范围．

正确答案

（1）；

（2）①证明略；②．

解析

（1）当=1时，A1=3，B1=1，从而可求得，

同理可得

（2）①当时，所以

当时，

两式相减得所以

又

所以，数列是以为首项、为公比的等比数列．

②由①知：；

又，

由于

所以由推得

所以对任意的正整数恒成立．

因为所以

由，得，

但且，所以解得，所以

考查方向

本题考查数列的综合应用，突出考查考查推理论证与抽象思维的能力，是难题．数列的综合应用在近几年各省市的高考试卷中频频出现，是高考的热点问题，往往以等差数列、等比数列为载体，涉及递推公式、通项公式、前项和，结合数列单调性、数列恒成立等知识交汇命题．

解题思路

题（1），当=1时，A1=3，B1=1，从而可求得，同理可求得的值；

题（2）①，利用等比数列的定义证明是等比数列，对含有的表达式，先利用（）求得与递推关系，将代入递推关系化简求得，同时验证的初始值，从而证明是等比数列；

题（2）②，由①得到的通项公式，根据求得，从而得到关于不等式，解得的取值范围．

易错点

对含有的表达式，往往利用求通项时容易忽视的要求，同时要验证的初始值；对新定义、的不理解；恒成立问题的恰当转化．

知识点

等比数列的判断与证明数列与不等式的综合

1

题型：简答题

|

简答题 · 10 分

28．已知数列的前项的和，

（1）求的通项公式；

（2）当时，恒成立，求的取值范围.

正确答案

an=3n-2;

解析

（1）

当时也成立,

（2）

设

的最小值为,.

考查方向

本题主要考查数列的综合运算

解题思路

1、求出an；

2、利用公式分离出λ，即可得到结果。

易错点

本题易在分离λ时发生错误。

知识点

由递推关系式求数列的通项公式数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

32．已知两个无穷数列分别满足，，其中，设数列的前项和分别为，

（1）若数列都为递增数列，求数列的通项公式；

（2）若数列满足：存在唯一的正整数（），使得，称数列为“坠点数列”

①若数列为“5坠点数列”，求；

②若数列为“坠点数列”，数列为“坠点数列”，是否存在正整数，使得，若存在，求的最大值；若不存在，说明理由。

正确答案

an=2n-1; ；；的最大值为。

解析

（1）数列都为递增数列，∴，，

∴，

；

（2）①∵数列满足：存在唯一的正整数，使得，且，

∴数列必为，即前4项为首项为1，公差为2的等差数列，从第5项开始为首项5，公差为2的等差数列，

故；

② ∵，即，

而数列为“坠点数列”且，∴数列中有且只有两个负项．

假设存在正整数，使得，显然，且为奇数，而中各项均为奇数，∴必为偶数

i.当时，

当时，，故不存在，使得成立

ii.当时，

显然不存在，使得成立

iii．当时，

当时，才存在，使得成立

所以

当时，，构造：为，为

此时，，所以的最大值为。

考查方向

本题主要考查数列的综合运算

解题思路

1、求出an，bn;

2、利用定义求解，即可得到结果。

易错点

本题易在利用新定义求解时发生错误。

知识点

由递推关系式求数列的通项公式等差数列的基本运算等比数列的基本运算数列与不等式的综合

1

题型：简答题

|

简答题 · 12 分

18.设数列{an}的前n项和为Sn，己知a1=l，nan+1=(n+2)Sn，n∈N*.求证：是等比数列；设Tn= S1+S2+--+Sn，求证：(n+l) Tn<nSn+1．

正确答案

（1）；

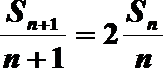
（2）略．

解析

本题属于数列中的基本问题，题目的难度是逐渐由易到难．

（1）由已知得。所以是以1为首项，2为公比的等比数列。

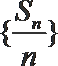
（2）由上知。

……①

……②

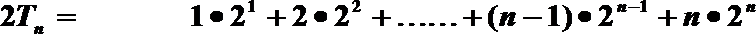
①-②得：。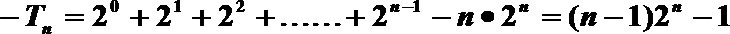

即(n+l) Tn<nSn+1．

考查方向

本题考查了数列的问题．属于高考中的高频考点。

易错点

错位相减法求和时相减的结果项数易错。

知识点

等比数列的判断与证明数列与不等式的综合

1

题型：简答题

|

简答题 · 16 分

22．已知数列与满足，.

（1）若，且，求数列的通项公式；

（2）设的第项是最大项，即（），求证：数列的第项是最大项；

（3）设，（），求的取值范围，使得有最大值与最小值，且.

正确答案

（1）

（2）详见解析

（3）

解析

因为，，所以，即.

故的第项是最大项.

（3）因为，所以，

当时，

.

当时，，符合上式.

所以.

因为，所以，.

①当时，由指数函数的单调性知，不存在最大、最小值；

②当时，的最大值为，最小值为，而；

③当时，由指数函数的单调性知，的最大值，最小值，由及，得.

综上，的取值范围是.

知识点

由递推关系式求数列的通项公式数列与函数的综合数列与不等式的综合

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

知识点