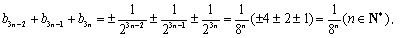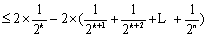- 数列求和、数列的综合应用
- 共491题
17. 如图,一质点

















正确答案
解析
探究


知识点
10.设函数

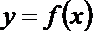
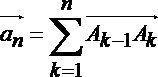
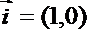
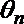
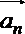
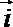
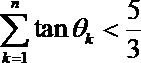
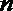
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
数列


正确答案
解析
略
知识点
对于数列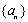
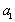
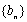
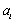
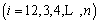
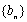
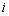
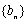
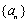
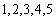
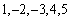
已知数列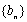
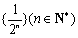
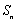
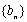
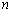
(1)写出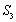
(2)若生成数列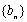
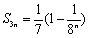
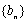
(3)证明:对于给定的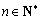
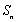
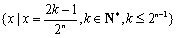
正确答案
见解析
解析
(1)由已知,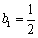
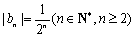
∴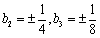
由于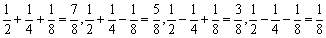
∴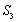
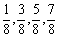
(2)∵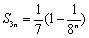
当
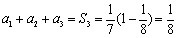
当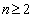
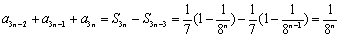
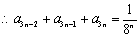
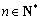
∵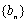
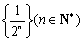
∴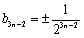
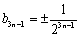
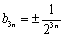
∴
在以上各种组合中,
当且仅当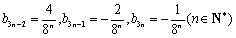
∴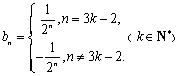
(3)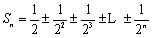
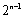
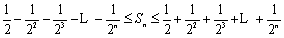
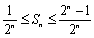
又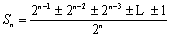
满足条件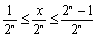
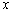
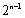
设数列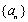
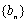
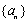
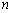
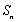
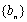
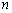
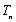
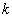
由于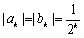
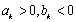
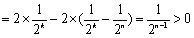
所以,只有当数列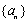
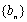
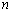
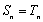
∴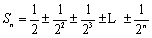
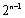
∴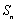
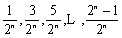
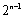
即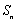
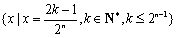
知识点
设等差数列{an}的公差d≠0,数列{bn}为等比数列,若a1=b1=a,a3=b3,a7=b5
(1)求数列{bn}的公比q;
(2)将数列{an},{bn}中的公共项按由小到大的顺序排列组成一个新的数列{cn},是否存在正整数λ,μ,ω(其中λ<μ<ω)使得λ,μ,ω和cλ+λ,cμ+μ,cω+ω均成等差数列?若存在,求出λ,μ,ω的值,若不存在,请说明理由。
正确答案
见解析。
解析
(1)设{bn}的公比为q,由题意
q=1不合题意,故

∴q=±
(2)若{an}与{bn}有公共项,不妨设an=bm,
由(2)知:m为奇数,且n=
令m=2k﹣1(k∈N*),则bm=a•
∴cn=2n﹣1a
若存在正整数λ,μ,ω(其中λ<μ<ω)满足题意,
设p=λ,q=μ,r=ω则
∴2q=2p﹣1+2r﹣1,又2p﹣1+2r﹣1≥2

又p≠r,
∴又2p﹣1+2r﹣1>
又y=2x在R上增,
∴q>

∴不存在λ,μ,ω满足题意。
知识点
已知


(1)求数列
(2)求数列的前n项和
正确答案
见解析。
解析
(1)由题设知公差d≠0
由

解得d=1,d=0(舍去)
故
(2)由(1)知
知识点
设



(1)求数列
(2)证明:对任意

正确答案
见解析
解析
(1)设数列


由


由




(2)证法一:对任意

所以,对任意

证法二:对任意



因此,对任意

知识点
已知数列

(1)求数列
(2)若p,q,r是三个互不相等的正整数,且p,q,r成等差数列,试判断
是否成等比数列?并说明理由。
正确答案
见解析。
解析
(1) 解:
∴ 当


由
得
② - ①得: 
以下提供两种方法:
法1:由③式得:
即

∵
∴数列
∴

当

又
∴
法2:由③式得:
得
当

⑤-④得:
由

∴
∴数列


(2)解:∵
∴
假设
则
即
化简得:
∵
∴
∴
知识点
在公差为



(1)求
(2)若
正确答案
(1)
(2)
解析
(1)由已知得到:


(2)由(1)知,当

①当
②当
所以,综上所述:
知识点
用部分自然数构造如图的数表:用



(1)写出
(2)令

(3)数列

正确答案
见解析
解析
知识点
扫码查看完整答案与解析