数列求和、数列的综合应用
共491题

数列求和、数列的综合应用
共491题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15．由9个正数组成的数阵每行中的三个数成等差数列，且，，成等比数列．给出下列结论：

①第二列中的必成等比数列；

②第一列中的不一定成等比数列；

③；

④若9个数之和大于81，则 >9．

其中正确的序号有．（填写所有正确结论的序号）．

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的判断与证明等比数列的性质及应用等差数列与等比数列的综合

题型：填空题

填空题 · 5 分

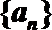
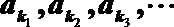
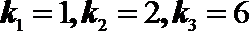
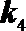
13．公差不为0的等差数列的部分项，构成等比数列，且，则= 。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列与等比数列的综合

题型：简答题

简答题 · 12 分

16．已知数列是等差数列，是等比数列，。

（1）求数列、的通项公式；

（2）设数列中，，求数列的前n项和Sn。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项错位相减法求和等差数列与等比数列的综合

题型：简答题

简答题 · 12 分

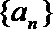
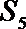
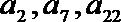
18．已知等差数列的公差不为零，其前n项和为，若=70，且成等比数列

（Ⅰ）求数列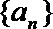的通项公式；

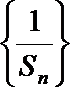
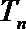
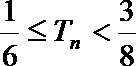
（Ⅱ）设数列的前n项和为，求证：。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项裂项相消法求和数列与不等式的综合等差数列与等比数列的综合

题型：简答题

简答题 · 12 分

19．公差不为零的等差数列中，已知其前n项和为，若，且成等比数列

（Ⅰ）求数列的通项;

（Ⅱ）当时，求数列的前n和．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

裂项相消法求和等差数列与等比数列的综合

题型：简答题

简答题 · 12 分

19．已知单调递增的等比数列满足：且的等差中项。

（I）求数列的通项公式；

（II）若成立的正整数n的最小值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项错位相减法求和数列与不等式的综合等差数列与等比数列的综合

题型：简答题

简答题 · 14 分

20．已知数列{}的前n项和为，且，数列{}为等比数列，且。

（1）求数列{}，{}的通项公式；

（2）若数列{}满足，求数列{}的前n项和；

（3）在（2）的条件下，数列{}中是否存在三项，使得这三项成等差数列，若存在，求出此三项；若不存在，说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项等差数列的判断与证明分组转化法求和等差数列与等比数列的综合

题型：简答题

简答题 · 16 分

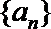
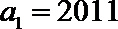
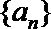
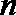
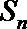
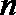
20．已知等比数列的首项，公比，数列前项和记为，前项积记为

（1）证明：；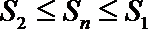

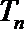
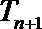
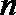
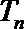
（2）判断与的大小，并求为何值时，取得最大值；

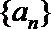
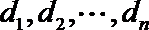
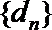
（3）证明：若数列中的任意相邻三项按从小到大排列，则总可以使其成等差数列；若所有这些等差数列的公差按从小到大的顺序依次记为，则数列为等比数列。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用数列与不等式的综合等差数列与等比数列的综合

题型：填空题

填空题 · 5 分

9.等差数列与等比数列中，若，则的大小关系是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

数列与不等式的综合等差数列与等比数列的综合

题型：单选题

单选题 · 5 分

5.已知数列{an}满足a1=1,an=logn（n+1）（n≥2,n∈N*）.定义:使乘积a1·a2·…·ak为正整数的k（k∈N）叫作“酷数”.则在[1,2016]内所有“酷数”的和为（　　）.

A2034

B2035

C2036

D2037

正确答案

解析

∵an=logn(n+1),∴a1·a2·a3·…·an=1×log23×log34×…×logn(n+1)=×××…×==log2(n+1),要使log2(n+1)为整数,则n+1=2k.在[1,2016]内所有整数分别为21-1,22-1,…,210-1.

则在[1,2016]内所有“酷数”的和为21-1+22-1+…+210-1=-10=2036

知识点

对数的运算性质等差数列与等比数列的综合

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 数列求和、数列的综合应用

扫码查看完整答案与解析