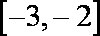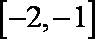- 集合与常用逻辑用语
- 共2295题
已知全集
A
B
C
D
正确答案
解析
由图可以得到阴影部分表示的集合为
知识点
已知集合
A
B
C
D
正确答案
解析
知识点
设全集
A
B
C
D
正确答案
解析
集合
知识点
已知全集U=R，集合M={x|﹣2≤x＜2}，P={x|y=
正确答案
解析
∵p={x|x≥0}，∴CUP={x|x＜0}，
∴M∩（∁UP）={x|﹣2≤x＜0}，
故选：A.
知识点
2.已知集合
AR
B{-1,0,1,2}
C
D{-1,0,2}
正确答案
解析
因为
知识点
2.已知集合A={x|x2≥1}，B={x|y=
正确答案
解析
由A中不等式解得：x≥1或x≤﹣1，即A=（﹣∞，﹣1]∪[1，+∞），由B中y=
故选：B。
知识点
1.若全集U=R，集合A={x|x2+x﹣2≤0}，B={y|y=log2（x+3），x∈A}，则集合A∩（∁UB）=（ ）
正确答案
解析
A={x|x2+x﹣2≤0}={x|﹣2≤x≤1}，
∵B={y|y=log2（x+3），x∈A}，由于函数y=log2（x+3）为增函数，
∴B={y|0≤y≤2}，
∵全集U=R∴∁UB={y|y＜0或y≥2}，∴A∩∁UB={x|﹣2≤x＜0}．故选：A．
知识点
1.已知集合
正确答案
解析
知识点
4.设f(x)是定义在R上的奇函数，其f(x)=f(x-2),若f(x)在区间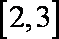
Af(x)在区间
Bf(x)在区间
Cf(x)在区间
Df(x)在区间
正确答案
解析
由f（x）=f（x﹣2），则函数的周期是2，
若f（x）在区间[2，3]单调递减，则f（x）在区间[0，1]上单调递减，
∵f（x）是定义在R上的奇函数，
∴f（x）在区间[﹣1，0]上单调递减，且f（x）在区间[1，2]上单调递减，
故选：D
知识点
1.若全集U=R，集合A={x|x2+x﹣2≤0}，B={y|y=log2（x+3），x∈A}，则集合A∩（∁UB）=（ ）
正确答案
解析
A={x|x2+x﹣2≤0}={x|﹣2≤x≤1}，
∵B={y|y=log2（x+3），x∈A}，由于函数y=log2（x+3）为增函数，
∴B={y|0≤y≤2}，
∵全集U=R
∴∁UB={y|y＜0或y≥2}，
∴A∩∁UB={x|﹣2≤x＜0}．
故选：A.
知识点
1.设集合A＝{(x，y)|x＋y＝1}，B＝{(x，y)|x－2y＝3}，则满足M⊆(A∩B)的集合M的个数是( )
正确答案
解析
由题中集合可知，集合A表示直线x＋y＝1上的点，集合B表示直线x－2y＝3上的点，联立
知识点
1.已知集合
AR
B{-1,0,1,2}
C
D{-1,0,2}
正确答案
解析
因为
知识点
9.已知全集
正确答案
解析
略
知识点
21.已知函数
（1）当
（2）若
（3）求证：
正确答案
见解析。
解析
（1）
（2） 因为
因为若
即
当
②当
③当
即方程
因为
所以方程
当
综合①②③知：
（3）（法一）根据（1）的结论，当
令
（法二）当
设当
根据（1）的结论，当
令
则有
因此，由数学归纳法可知不等式成立．
知识点
13.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作，若其中甲、乙两名志愿者不能从事翻译工作，则选派方案共有________.
正确答案
240种
解析
根据题意，由排列可得，从6名志愿者中选出4人分别从事四项不同工作，有A＝360种不同的情况，其中包含甲从事翻译工作，有A＝60种，乙从事翻译工作，有A＝60种，若其中甲、乙两名志愿者都不能从事翻译工作，则选派方案共有360－60－60＝240种.
知识点
扫码查看完整答案与解析