集合与常用逻辑用语_章节学习

1

题型：简答题

|

简答题 · 12 分

18．设命题P：关于x的不等式a>1（a>0且a≠1）为{x|-a<x<2a}；命题Q：y=lg（ax-x+a）的定义域为R。如果P或Q为真，P且Q为假，求a的取值范围

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用含有逻辑联结词命题的真假判断对数函数的定义域一元二次不等式的解法

1

题型：简答题

|

简答题 · 12 分

19. 如图，四棱锥中，底面为菱形，，是的中点.

（1）若，求证：；

（2）若平面，且点在线段上，试确定点的位置，使二面角的大小为，并求出的值.

正确答案

（1），为的中点，，

又底面为菱形，，

,

又

平面，

又平面,

平面平面;

（2）平面平面,平面平面,

平面.

以为坐标原点，分别以为轴建立空间直角坐标系如图.

则,设(),

所以，平面的一个法向量是，

设平面的一个法向量为，所以

取，

由二面角大小为，可得：

，解得，此时

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：简答题

|

简答题 · 14 分

20．已知某地今年年初有居民住房的总面积为（单位：），其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房，同时也拆除面积为（单位：）的旧住房。

（1）分别写出第一年末和第二年末的实际住房面积的表达式；

（2）如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%，则每年拆除的旧住房面积是多少？（计算时取）

正确答案

（1）第1年末的住房面积：

第2年末的住房面积：

（2）第3年末的住房面积：

第4年末的住房面积：

第5年末的住房面积：

=

由题意可知，，解得

所以每年拆除的旧房面积为

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

17．已知为平面内一定点，设条件:动点满足，;

条件:点的轨迹通过△的重心．则条件是条件的（）

A充要条件

B必要不充分条件

C充分不必要条件

D既不充分也不必要条件

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：简答题

|

简答题 · 15 分

22．设函数的导函数为，若，则称点是函数的一个驻点。已知函数

（1）若函数总存在有两个驻点，求所满足的关系；

（2）若函数有两个驻点，且存在，求两个驻点在不等式表示的区域内时实数的范围；

（3）若函数恰有一个驻点，且存在，使驻点在不等式表示的区域内，证明：.

正确答案

解：（1）

令得又

（2）在有两个不相等的实根.

即得

所以

（3）由①

①当，在左右两边异号

是的唯一的一个驻点

由题意知即即

存在这样的满足题意

符合题意

②当时，即

这时函数唯一的一个驻点为

由题意

即即

综合①②知：满足题意的范围为.

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

11. 求形如的函数的导数，我们常采用以下做法：先两边同取自然对数得：,再两边同时求导得，于是得到：，运用此方法求得函数的一个单调递增区间是( )

A(e,4)

B(3,6)

C(0,e)

D(2,3)

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

12.若，则下列结论不正确的是（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

10．已知函数，则的值域为（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

2．设复数在复平面内对应的点关于原点对称，，则=（）

A－2i

B2i

C－2

D2

正确答案

A

解析

在复平面内的对应点为，它关于原点对称的点为，故，所以则选A．

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 4 分

16．设[x]表示不超过x的最大整数（例如：[5．5]=5，[一5．5]＝－6），则不等式的解集为（）

A（2，3）

B[2，4]

C[2，3]

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

3．设命题：，则为（）

A

B

C

D

正确答案

C

解析

:，故选C.

考查方向

本题主要考查特称命题的否定，属于基础题.

解题思路

在特称命题否定为全称命题时要注意，转化为，>转化为即可。

易错点

本题易在特称、全称命题的转化过程中出错.

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

3．给定下列两个命题：

①“p∨q”为真是“¬p”为假的必要不充分条件；

②“xR，使sinx＞0”的否定是“xR，使sinx0”．

其中说法正确的是( )

A①真②假

B①假②真

C①和②都为真

D①和②都为假

正确答案

C

解析

对于命题1，由¬p为假可以推出p∨q为真，但由p∨q为真不能推出¬p为假的值，所以前者是后者的必要不充分条件，命题1正确。易得命题2也是正确的。所以选C

考查方向

命题真假的判断；充分条件；必要条件

解题思路

根据相关性质，逐一判断

易错点

对逻辑与命题理解不透彻；

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

1

题型：填空题

|

填空题 · 5 分

4. 若角的终边落在射线上，则=（）

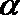
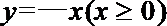
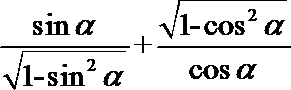
正确答案

0

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

2．已知两点，则与同方向的单位向量是（）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

1

题型：单选题

|

单选题 · 5 分

4．设命题p：“若，则”，命题q：“若，则”，则（）

A“”为真命题

B“”为真命题

C“”为真命题

D以上都不对

正确答案

B

解析

对于命题p:由函数为增函数且当x=0时y=1知若，则，故其为真命题；对q:命题由a=1,b=-1代入验证知验证得出不成立，故其为假命题。然后由复合命题真值表得出“”为真命题。故选B

考查方向

本题主要考查简单命题真假性的判断和复合命题真值表的运用、不等式的性质以及函数思想的应用，综合性较强，侧重对学生函数思想的应用及逻辑推理能力的考查。

解题思路

对于命题p:真假性的判断可利用函数的单调性辅助解决，即：构造函数由其为增函数且当x=0时y=1知其为真命题；对q:命题真假性判断时可运用特值验证的办法验证得出其为假命题。然后由复合命题真值表得出“”为真命题。

易错点

本题易在命题q:的真假性判断时忽略a,b的正负号而得出错误的结论。

知识点

含有逻辑联结词命题的真假判断

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点