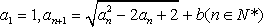- 集合与常用逻辑用语
- 共2295题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
下列命题中错误的是
正确答案
解析
因为若这条线是





知识点
设
(1)若
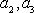
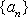
(2)若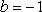

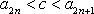
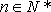
正确答案
(1)an=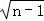
(2)存在,c=
解析
(1)∵a1=1,an+1=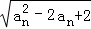
∴a2=2,a3=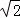
又(an+1﹣1)2=(an﹣1)2+1,
∴{(an﹣1)2}是首项为0,公差为1的等差数列;
∴(an﹣1)2=n﹣1,
∴an=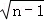
(2)设f(x)=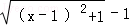
令c=f(c),即c=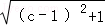
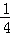
下面用数学归纳法证明加强命题a2n<c<a2n+1<1。
n=1时,a2=f(1)=0,a3=f(0)=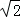
设n=k时结论成立,即a2k<c<a2k+1<1
∵f(x)在(﹣∞,1]上为减函数,
∴c=f(c)>f(a2k+1)>f(1)=a2,
∴1>c>a2k+2>a2,
∴c=f(c)<f(a2k+2)>f(a2)=a3,<1,
∴c<a2k+3<1,
∴a2(k+1)<c<a2(k+1)+1<1,即n=k+1时结论成立,
综上,c=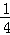
知识点
如图,圆








正确答案
8
解析
略
知识点
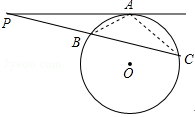
过圆外一点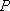
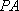
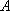
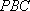
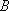
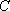
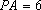
正确答案
解析
由题意,∠PAB=∠C,∠APB=∠CPA,
∴△PAB∽△PC由题意,∠PAB=∠C,∠APB=∠CPA,
∴△PAB∽△PCA,
∴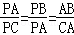
∵PA=6,AC=8,BC=9,
∴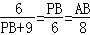
∴PB=3,AB=4,故答案为4。
知识点
如图,在复平面内,点A表示复数z,则图中表示z的共轭复数的点是( )。
正确答案
解析
知识点
已知函数
(1)求
(2)若对任意的



(3)证明

正确答案
见解析
解析
(1)


当


因此,

取得最小值,故由题意
(2)当



当

令
①当









②当

故




故
(3)证明:当

当
在(2)中取

所以有
综上
知识点
若平面向量


正确答案
﹣
解析
∵平面向量

∴
∴




∴
∴
故

知识点
已知函数f(x)=x(1+a|x|),设关于x的不等式f(x+a)<f(x)的解集为A.若
正确答案
解析
f(x)=x(1+a|x|)=
若不等式f(x+a)<f(x)的解集为A,且
则在区间
(1)当a=0时,显然不符合条件。
(2)
当a>0时,画出函数y=f(x)和y=f(x+a)的图象大致如图。
由图可知,当a>0时,y=f(x+a)的图象在y=f(x)图象的上边,故a>0不符合条件。
(3)
当a<0时,画出函数y=f(x)和y=f(x+a)的图象大致如图。
由图可知,若f(x+a)<f(x)的解集为A,且
只需
则有
整理,得a2-a-1<0,解得
∵a<0,∴a∈
综上,可得a的取值范围是
知识点
设集合

正确答案
解析
略。
知识点
已知M是集合





正确答案
3;
解析
略
知识点
定义全集U的子集P的特征函数

①若

②对于任意
③对于任意
④对于任意
正确答案
解析
略
知识点
已知全集U=R,集合
正确答案
解析
略
知识点
5.不等式|x-1|-|x-5|<2的解集是()
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析