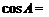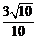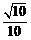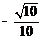- 求函数y=Asin(ωx+φ)的解析式
- 共155题
21.[选做题]本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.

正确答案
A 由

由


则
由

由

因此
又

B 
C 直线



联立得


因此
D 由

知识点
6.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
正确答案
知识点
7.将函数


正确答案
知识点
7.已知△ABC是边长为1的等边三角形,点D、E分别是边AB、BC的中点,连接DE并延长到点F,使得DE=2EF,则
正确答案
知识点
8.在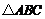
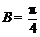
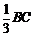
正确答案
知识点
已知函数f(x)= 

25.求函数f(x)的最小正周期及单调减区间;
26.把函数f(x)的图像向右平移
正确答案
T=



解析
f(x)=sin(2x-2φ)-+=sin(2x-2φ)-cos(2x-2φ)=sin(2x-2φ-

















解题思路
先用二倍角公式和降幂公式化简,然后用辅助角公式合二为一,再求最小正周期和单调减区间
易错点
降幂公式不会用,忘记写k属于整数,对称中心不知道写成点的坐标的形式。
正确答案
g(x)的对称中心为(
解析
函数f(x)=-cos2x的图像向右平移







考查方向
解题思路
利用平移变换左加右减得到另一个函数的解析式,再求出其对称中心。
易错点
降幂公式不会用,忘记写k属于整数,对称中心不知道写成点的坐标的形式。
3.已知

正确答案
解析

考查方向
解题思路
利用诱导公式进行转换
易错点
变换时没有注意到角度的取值范围
知识点
5.若函数


正确答案
解析
∵

由



∴


考查方向
本题主要考查了三角函数与二次函数的复合函数性质以及二倍角公式的应用研究,在近几年的各省高考题出现的频率较高,常以三角公式与三角函数等知识综合命题,较难。
解题思路
1、先根据题意把原题化为
2、依题意


易错点
1、本题由于无法把题意理解成复合函数的考查而无法下手导致出错。
2、本题易忽视换元后
知识点
已知函数
17.求
18.在


正确答案
解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。
(1)求解时一定要三角公式的应用研究及辅助角公式的正确应用;
(2)在周长的范围时切记不要忘记三角形中边角关系的转换。
由
易知
由

∴

考查方向
本题考查了三角函数的性质及和角公式在三角函数化简中的应用,考查了三角形中的三边关系、给定区间求三角函数最值等基础知识,意在考查考生的运算求解能力.
解题思路
本题考查了三角函数的性质及和角公式在三角函数化简中的应用,解题步骤如下:
1、分析判断后化

2、由(1)算出角B,再把计算周长最大值转化成给定区间求三角函数最大值问题。
易错点
1、第一问化简
2、第二问给定区间求三角函数最值时未考虑范围而出错。
正确答案
解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。
(1)求解时一定要三角公式的应用研究及辅助角公式的正确应用;
(2)在周长的范围时切记不要忘记三角形中边角关系的转换。
∵

∵


在


∴

∵

故当



考查方向
本题考查了三角函数的性质及和角公式在三角函数化简中的应用,考查了三角形中的三边关系、给定区间求三角函数最值等基础知识,意在考查考生的运算求解能力.
解题思路
本题考查了三角函数的性质及和角公式在三角函数化简中的应用,解题步骤如下:
1、分析判断后化

2、由(1)算出角B,再把计算周长最大值转化成给定区间求三角函数最大值问题。
易错点
1、第一问化简
2、第二问给定区间求三角函数最值时未考虑范围而出错。
19.已知非单调数列



(Ⅰ)求
(Ⅱ)若对任意正整数


(Ⅲ)设数列





正确答案
(1)
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.



2)
当
当




3)




考查方向
解题思路
本题考查数列问题,解题步骤如下:1、利用等比数列公式求解。2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
扫码查看完整答案与解析