求函数y＝Asin(ωx＋φ)的解析式
共155题

· 求函数y＝Asin(ωx＋φ)的解析式

求函数y＝Asin(ωx＋φ)的解析式
共155题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

在如图所示的几何体中，四边形ABCD为矩形，平面ABEF⊥平面ABCD， EF // AB，∠BAF=90º， AD= 2，AB=AF=2EF =1，点P在棱DF上。

（1）若P是DF的中点，求异面直线BE与CP所成角的余弦值；

（2）若二面角D-AP-C的余弦值为，求PF的长度。

正确答案

（1）

（2）

解析

（1）因为∠BAF=90º，所以AF⊥AB，

因为平面ABEF⊥平面ABCD，且平面ABEF ∩平面ABCD= AB，

所以AF⊥平面ABCD，因为四边形ABCD为矩形，

所以以A为坐标原点，AB，AD，AF分别

为x，y，z轴，建立如图所示空间直角坐标系。

所以，，，。

所以，，

所以，

即异面直线BE与CP所成角的余弦值为。

（2）因为AB⊥平面ADF，所以平面APF的法向量为。

设P点坐标为，在平面APC中，，，

所以平面APC的法向量为，

所以，

解得，或（舍）。

所以。

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 15 分

在中，内角的对边长分别为，且满足，.

（1）求的值；

（2）若，求的面积.

正确答案

见解析

解析

解：（1）由，

所以，-

因为，

所以

（2）由已知得

因为，所以由正弦定理得

，解得.

所以的面积.

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 4 分

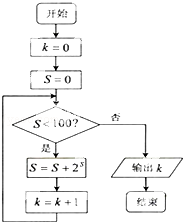
执行如图所示的程序框图，则输出的k=　　。

正确答案

解析

解：分析程序中各变量、各语句的作用，

再根据流程图所示的顺序，

可知：该程序的作用是：

输出不满足条件S=0+1+2+8+…＜100时，k+1的值。

∵当k=3时，1+2+8=11＜100

而当k=4时，1+2+8+211＞100

故最后输出k的值为4

故答案为：4

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 12 分

在平面直角坐标系中，已知点，向量，点B为直线上的动点，点C满足，点M满足.

（1）试求动点M的轨迹E的方程；

（2）设点P是轨迹E上的动点，点R、N在轴上，圆内切于，求的面积的最小值.

正确答案

见解析

解析

（1）设，则，

由得，所以动点M的轨迹E的方程为；……………4分

（2）设，且，，

即，由相切得，注意到，化简得

，

同理得，

所以是方程的两根，………………………………………………8分

所以，

有，当时的面积的最小值为8. …12分

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 12 分

已知函数的最小正周期为,当时，函数的最小值为0。

（1）求函数的表达式；

（2）在△ABC中，若的值。

正确答案

（1）

（2）

解析

（1）……2分

依题意函数

所以 …………4分

（2）

知识点

求函数y＝Asin(ωx＋φ)的解析式

继续学习学习下一知识点

下一知识点 : 函数y＝Asin(ωx＋φ)的应用

百度题库 > 高考 > 理科数学 > 求函数y＝Asin(ωx＋φ)的解析式

扫码查看完整答案与解析