- 双曲线及其性质
- 共531题
9.已知点











正确答案
解析
由题意得:





考查方向
解题思路
(1)已知渐近线方程y=mx,若焦点位置不明确要分





易错点
双曲线焦点所在坐标轴
知识点
3.若双曲线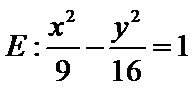
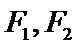
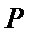
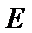
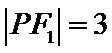

正确答案
解析
由双曲线定义得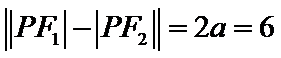
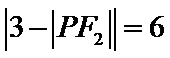
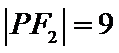
考查方向
解题思路
确定P在双曲线的左支上,由双曲线的定义可得结论。
易错点
计算能力弱,双曲线焦点坐标不会求
知识点
6.若双曲线
正确答案
解析
由题意得


考查方向
解题思路
直接根据题意得到a,b,c之间的关系即可得到答案。
易错点
弄错渐近线方程导致结果出错。
知识点
10.已知双曲线


正确答案
解析
将


考查方向
解题思路
本题考查运用双曲线的渐近线方程及抛物线的准线方程,求a,b,解题步骤如下:将



易错点
本题必须注意审题,忽视则会出现错误。
知识点
16.在双曲线
正确答案
解析
由题意,F(c,0),B(0,b),则直线BF的方程为bx+cy-bc=0,若在线段BF上存在点P,使得△PA1A2构成以A1A2为斜边的直角三角形,则

考查方向
解题思路
根据题意写出线段BF所在直线方程,借助△PA1A2构成以A1A2为斜边的直角三角形构建原点到直线的距离小于或等于a,从而解出e的取值范围。
易错点
△PA1A2构成以A1A2为斜边的直角三角形的转化
知识点
10.在平面直角坐标系xOy中,抛物线y2=2px(p>0) 的焦点为F,双曲线
正确答案
y=±2x
解析
抛物线y2=2px(p>0)的焦点为F
双曲线

代入抛物线的方程,可得A
由A,B,F三点共线,可得:
考查方向
解题思路
求得抛物线的焦点,双曲线的渐近线方程,代入抛物线的方程可得A,B,再由A,B,
F共线,可得
易错点
混淆抛物线和双曲线的几何性质,同时计算容易出现错误
知识点
7.过双曲线


正确答案
解析
由题意得 F(c,0 ),由切点为M为线段FP的中点可知,OM是△FOP的底边FP的中线也是高线,故FPO为等腰直角三角形,∴点P(0,c ),由中点公式得M


∴所以选项C为正确选项
考查方向
解题思路
判断FPO为等腰直角三角形,由中点公式得M
易错点
本题易在无法判断FPO为等腰直角三角形,找不出等量关系
知识点
11.已知A,B为双曲线E的左,右顶点,点M在E上,∆ABM为等腰三角形,且顶角120°,则E的离心率为( )
正确答案
知识点
8.过双曲线








正确答案
解析
由题意可知P(-1,0),所以直线L的方程为y=x+1,两条渐近线的方程为y=-bx或y=bx,所以可得Q点横坐标为

所以

C=

考查方向
解题思路
先求出R和Q的横坐标,然后求出b的值,进而求出c,然后根据离心率公式答案可得
易错点
计算能力弱,离心率公式记混淆
知识点
7.已知双曲线

正确答案
解析
利用抛物线的性质得出焦点为
所以双曲线方程为

考查方向
解题思路
1、利用抛物线的性质得出焦点为
2、根据双曲线的几何性质得出
3、根据双曲线的几何性质直接写出渐近线
易错点
本题主要易错于焦点位置的判断以及m的含义
知识点
扫码查看完整答案与解析





























