- 抛物线及其性质
- 共507题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若复数


正确答案
解析
C;

知识点
已知双曲线





正确答案
解析
略
知识点
设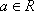
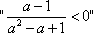
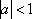
正确答案
解析
略
知识点
若直线









正确答案
解析
略
知识点
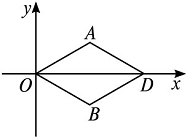
在平面直角坐标系中,O是坐标原点,两定点A,B满足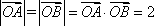
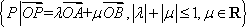
正确答案
解析
以






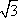
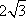
现设P(x,y),则由



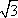
由于|λ|+|μ|≤1,λ,μ∈R,
可得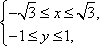
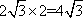
知识点
若抛物线

正确答案
解析
椭圆右焦点为
知识点
若抛物线


正确答案
解析

知识点
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点M的横坐标为



正确答案
见解析。
解析
(1)F抛物线C:x2=2py(p>0)的焦点F






(2)假设存在点M,使得直线MQ与抛物线C相切于点M,
而




由



即


(3)若点M的横坐标为


由


圆

于是

设

当

即当

故当

知识点
阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )
正确答案
解析
由程序框图知:算法的功能是求S=0+lg



∵S=lg







∴跳出循环的i值为9,∴输出i=9。
知识点
扫码查看完整答案与解析