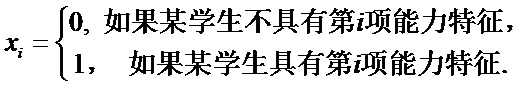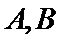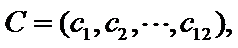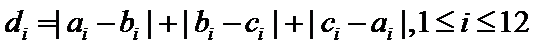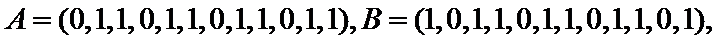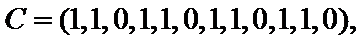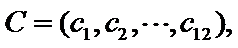- 排列、组合的实际应用
- 共39题
5.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为
正确答案
知识点
10.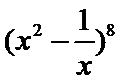
正确答案
-56
知识点
如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为
正确答案
知识点
11.

正确答案
解析





考查方向
解题思路
先求出二项式展开式的通项公式,再令X的次数等于2,求得r的值,即可得到展开式中的系数。
易错点
二项式展开错误,计算能力弱
知识点
14.某班主任在其工作手册中,对该班每个学生用十二项能力特征加以描述.每名学生的第
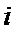
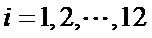
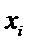
若学生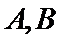
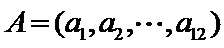
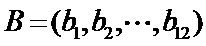
两名学生的不同能力特征项数为 (用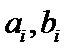
同学不同能力特征项数不少于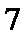
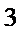
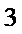
正确答案
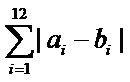
解析
设第三个学生为
因为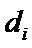
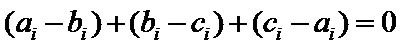
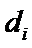
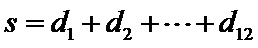
又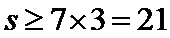
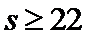
取
则不同能力特征项数总和恰为22 ,所以最小值为22 .
考查方向
解题思路
理解清题意即可得到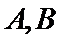
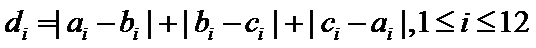
易错点
本题不易读懂题意,特别是对“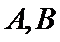
知识点
10.某校高三理科实验班有5名同学报名参加甲、乙、丙三所高校的自主招生考试,每人限报一所高校.若这三所高校中每个学校都至少有1名同学报考,那么这5名同学不同的报考方法种数共有( )
正确答案
解析
根据条件可以依据人数分为3,1,1和2,2,1两种情况,所有总数为
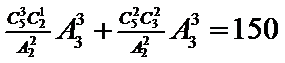
考查方向
解题思路
根据题目的要求所确定的方案确定分组的人数。
易错点
很容易因为均匀分组时忘记除以组数而出现错误。
知识点
9.


正确答案
20
解析
该二次项展开为






考查方向
解题思路
根据二项式展开式,求得
易错点
二项式展开后,忽略某几项乘积为
知识点
两个三口之家,共4个大人,2个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐4人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是 .
正确答案
48
解析
第一步:将两个小孩分别放在两辆车中,则是

考查方向
本题主要考查了排列组合的问题,也是常考题型
易错点
少算、多算是排列组合中最容易出错的问题
知识点
20.在数字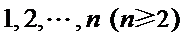
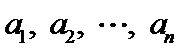
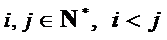
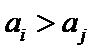
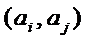
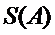
如
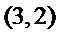
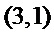
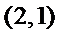
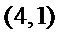
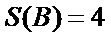
(Ⅰ)设排列 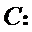
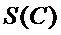
(Ⅱ)对于数字1,2,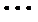
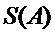
(Ⅲ)如果把排列A: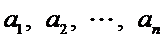

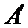
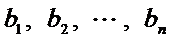
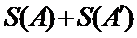
正确答案
(Ⅰ)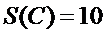
(Ⅱ)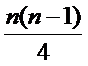
(Ⅲ)证明略。
解析
试题分析:本题属于新定义题目的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意分类讨论思想的应用
(Ⅰ)解: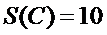
(Ⅱ)解:考察排列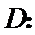
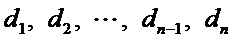
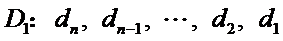
因为数对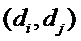
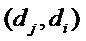
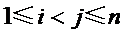
且排列D中数对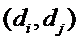
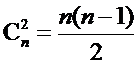
所以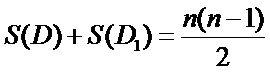
所以排列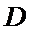
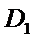
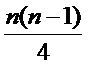
而对于数字1,2,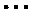
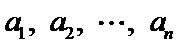
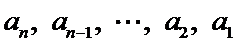
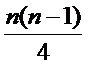
所以所有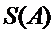
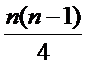
(Ⅲ)证明:①当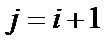
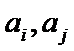
不妨设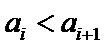
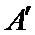
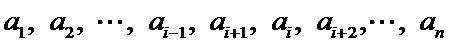
此时排列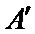
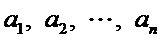

所以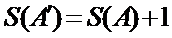
所以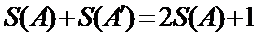
②当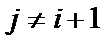
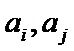
假设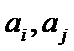
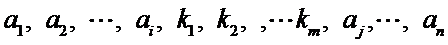
先将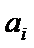
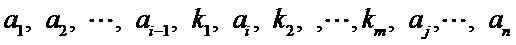
由①,知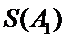
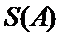
再将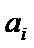
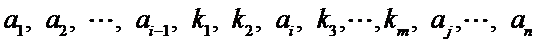
由①,知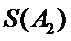
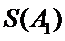
以此类推,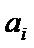
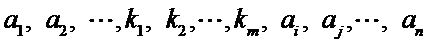
再将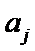
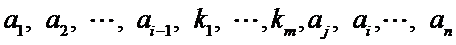
以此类推,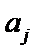
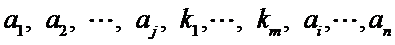
即为排列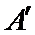
由①,可知仅有相邻两数的位置发生变化时,排列的逆序对个数的奇偶性发生变化,
而排列A经过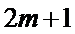
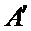
所以排列A与排列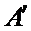
所以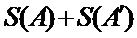
综上,得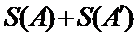
考查方向
本题主要考查了新定义的研究,对新定义问题的考查注意分以下几类:
1.与集合相关的新定义,
2.与数列相关的新定义,
3.与函数相关的新定义;与计数原理相关的新定义.
解题思路
本题考查新定义问题的考查,解题步骤如下:
1.直接写出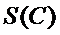
2.考查考察排列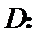
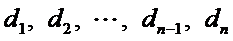
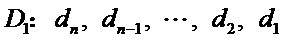
3.研究排列与逆序的个数,进而求其平均值;
4.分情况讨论研究“仅有相邻两数的位置发生变化”
易错点
1、第二问中,对“逆序”理解不透彻,导致错误;
2、第三问中,不要忽视对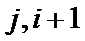
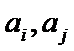
知识点
扫码查看完整答案与解析