- 解三角形的实际应用
- 共47题
14.路灯距地平面为8m,一个身高为1.75m的人以

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.集合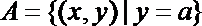
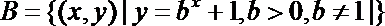
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在






(Ⅰ)当


(Ⅱ)若


正确答案
解:
(Ⅰ)由函数

解得
又


当

于是当



(Ⅱ)由正弦定理得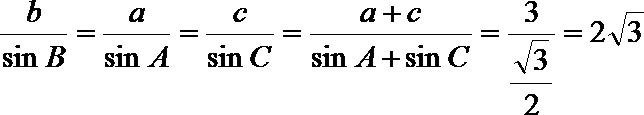
又

由余弦定理得
解得
于是

解析
解析已在路上飞奔,马上就到!
知识点
9.在









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.儿子身高为1.30米,在地面上选取C,D两点,儿子从C,D两点分别看我的头顶的仰角为30°,45°,且C,D两点间的距离为0.5 m,则我的高度约为( )(精确到0.01米)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)求函数
(2)在



正确答案
见解析
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
所以,函数

(2)∵ 在

∴ 
∴ 
∵ 
∴ 

∴
又由正弦定理得

∴
考查方向
解题思路
本题考查三角函数问题,解题步骤如下:1、利用辅助角公式及两角和差公式化简求最值。2、利用两角和差公式求解。
易错点
注意角度的范围,忽视则容易出错。
知识点
22.如图,在直角△ABC中,ABBC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.

(Ⅱ)若D为BC的中点,且AF=3,
正确答案
见解析
解析
(Ⅰ)连接EF、BE, 则∠ABE=∠AFE,
因为AB是⊙O的直径,所以AE⊥BE,
又因为AB⊥BC,所以∠ABE=∠C,
所以∠C=∠AFE, 即∠EFD + ∠C = 180º,
所以C,E,F,D四点共圆。
(Ⅱ)因为AB⊥BC,AB是⊙O的直径,
所以BC是⊙O的切线,DB2= DF×DA=4,即BD=2
所以AB
因为D是BC的中点,所以BC=4,AC
(方法一)因为C,E,F,D四点共圆,所以AE×AC=AF×AD.
即
(方法二)由CB2 = CE×CA,得
所以
考查方向
解题思路
解题步骤如下:要证明四点共圆,只需证明一组内角互补即可,在本题中,要求线段的长,可以考虑圆幂定理
易错点
本题易在用切割线定理时发生错误 ,导致题目无法进行。
知识点
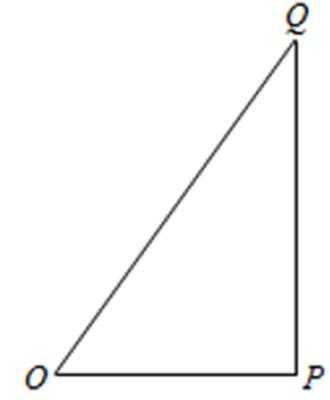
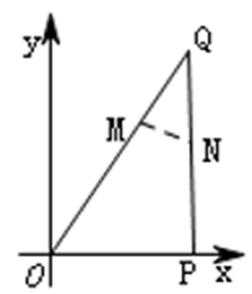
21.如图,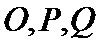
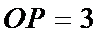
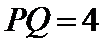
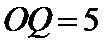
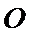
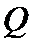
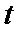
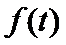
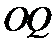
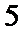
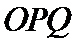
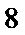
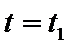
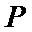
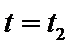

(1)求
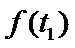
(2)已知警员的对讲机的有效通话距离是3千米,当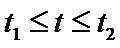
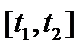
正确答案
(1)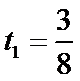
(2)见解析
解析
(1)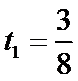
设乙到
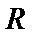
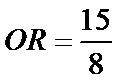
在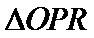
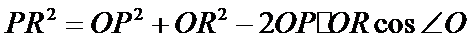
所以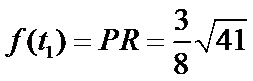
(2)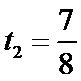
如图建立平面直角坐标系,
设经过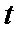
当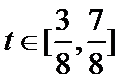
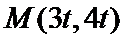
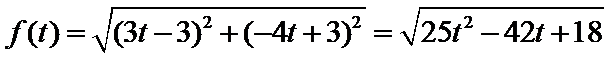
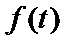
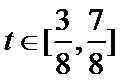
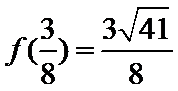
知识点
17. 在







(Ⅰ)求证:
(Ⅱ)若


正确答案
(Ⅰ)略;(Ⅱ)
解析
解:(Ⅰ)由条件:
由于:
所以:
(Ⅱ)


又:
由

所以:
考查方向
本题考查了三角函恒等变换及解三角形的有关知识,注意降幂公式的运用。第二问中要注意将角的关系和面积关系向边的关系的转化。
解题思路
第一小题中先降幂,再由余弦定理将角转化为边的关系;第二小题中由余弦求出正弦,再由面积得出边的关系;再由余弦定理得出另一个边的关系。从而求出b 的值。
易错点
第二问中由余弦值求正弦值不要忽略角的范围的限制,
知识点
扫码查看完整答案与解析