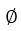- 不等式的应用
- 共30题
5.已知,
正确答案
知识点
设函数





26.求


27.设


正确答案

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,由函数的奇偶性形成方程组求解出



联立①②解得





考查方向
解题思路
本题考查导数的应用,解题步骤如下:函数的奇偶性形成方程组求解出
易错点
对求解析式方法不熟导致出错。
正确答案
详见解析;
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,由函数的奇偶性形成方程组求解出



联立①②解得





考查方向
解题思路
本题考查导数的应用,解题步骤如下:
观察所证不等式的结构构建新函数去证明所求不等式。
易错点
未发现
23.设数列




(Ⅰ)若

(Ⅱ)若

(Ⅲ)是否存在p和q,使得
正确答案
(Ⅰ)由题意,得
解
得
∴
即
(Ⅱ)由题意,得
由

根据


当

∴

(Ⅲ)假设存在p和q满足条件,
由不等式


∵
根据
对于任意的正整数m 都有

即
当

得

当

得
解得
∴ 存在p和q,使得
p和q的取值范围分别是

解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


正确答案
m≤-2
解析
令f(x)=(2-2-|x+2|)2,
要使f(x)=2+a有实根,
只需2+a是f(x)值域内的值.
∵f(x)的值域为[1,4),
∴1≤2+a<4,∴-1≤a<2.
知识点
3.已知6双袜子与3双手套的价格之和大于24元,而1双袜子与1双手套的价格之和小于5元,那么2双袜子和3双手套的价格的比较结果是( ).
正确答案
解析
设一双袜子与一双手套的价格分别为x,y元,则6x+3y>24,得2x+y>8,又x+y<5,所以2x-3y=5(2x+y)-8(x+y)>5×8-8×5=0,故2双袜子的价格高
知识点
函数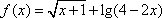
正确答案
解析
略
知识点
已知函数
(1)当

(2)若函数


(3)当


正确答案
(1)3(2)
解析
(1) 当

当

(2) 
依题意 

(3) 当




设
(1)当



(2)当


不妨设
当




不满足已知条件。
综上:

知识点
已知

正确答案
解析
∵sinθ+cosθ=﹣
∴(sinθ+cosθ)2=1+2sinθcosθ=
∴2sinθcosθ=sin2θ=﹣
又cos(2θ﹣
∴cos(2θ﹣


故选A,
知识点
已知集合M={x|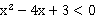
正确答案
解析
因为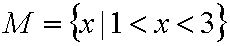
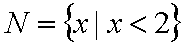
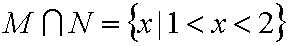
知识点
18. 某工厂某种产品的年固定成本为250万元,每生产



(1)写出年利润

(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
正确答案
(1)因为每件商品售价为0.05万元,则

依题意得:当


当


所以
(2)当
此时,当


当


即

所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析