- 不等式的应用
- 共30题
对于函数





已知函数
18.

若区间

正确答案
解析
解:(Ⅱ)
因为区间

考查方向
考察函数的新信息题,具体涉及到函数的定义域,值域,图像等性质
解题思路
先确定函数的值域,利用“可等域函数”, 结合函数的图象,可得函数 
易错点
对新信息理解到位易出错,对函数的综合性质应用不熟练易出现,分类与解题逻辑上的错误,数形结合应用易出错
正确答案
解析
考查方向
考察函数的新信息题,具体涉及到函数的定义域,值域,图像等性质
解题思路
利用“可等域区间”的定义,得出a>0,结合图象,利用区间与对称轴的关系及函数的单调性求出a,b
易错点
对新信息理解到位易出错,对函数的综合性质应用不熟练易出现,分类与解题逻辑上的错误,数形结合应用易出错
函数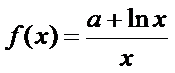
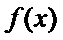

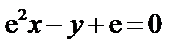
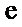

25.若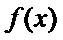
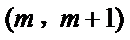


26.求证:当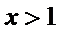
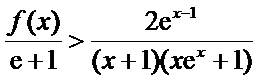
正确答案
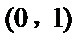
解析
因为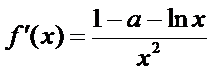
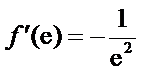
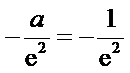
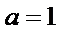
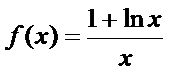
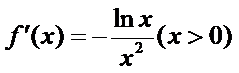
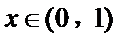
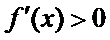
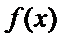
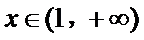
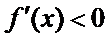
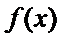
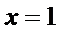
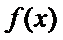
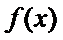
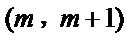
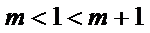
即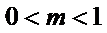
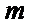
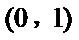
考查方向
解题思路
第一问由切线与直线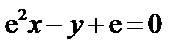
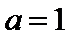
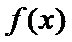
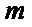
正确答案
略;
解析
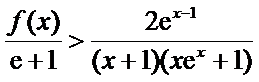
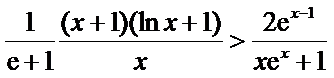
令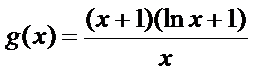
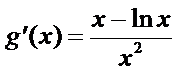
再令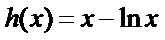
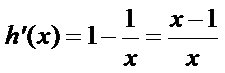
因为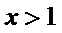
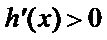
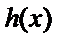
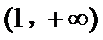
所以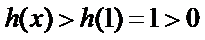
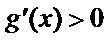
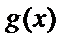
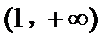
所以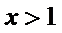
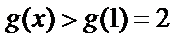

令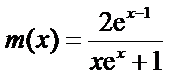

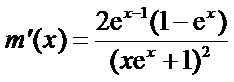
因为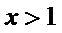
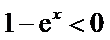
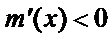
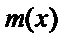
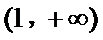
所以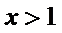
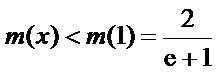
所以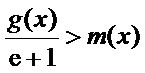
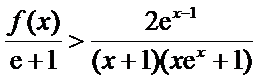
考查方向
解题思路
第二问现将不等式等级变形,构造新函数,对新函数用导函数求最值
13.在直角坐标系中,已知点







正确答案
4
解析
令a=0,则by



考查方向
解题思路
可令a=0 by



易错点
由可行域向不等式恒成立转化
知识点
已知函数
26.若函数

27.若函数

28.若



注:题目中e=2.71828…是自然对数的底数.
正确答案
(Ⅰ)
解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
(Ⅰ)



又



则切线l的方程又可表示为
由

考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
正确答案
(Ⅱ)
解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
a=
(Ⅱ)由题

令



则当x>0时,
由


考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
正确答案
(Ⅲ)

解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
(Ⅲ)

由题


当


因为


所以
同理
①+②得
因为
由


所以

所以

考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
设函数



25.求
26.证明:
正确答案
(1)

解析
试题分析: 本题属于导数的综合应用,考查考生转化与化归数学思想与方法。
(Ⅰ)因为


又点


所以

考查方向
解题思路
(1)利用导数解决曲线的切线问题,从而解出a,b的值
(2)通过构造新函数的方法找到证明不等式的突破口。
易错点
不等式证明如何构造新函数
正确答案
(2)对任意

解析
试题分析: 本题属于导数的综合应用,考查考生转化与化归数学思想与方法。
(Ⅱ)令
因为

所以




我们如果能够证明

下面证明:对任意

由(1)知
则


又



当



当



所以


所以
令
所以

所以
综上,对任意

考查方向
解题思路
(1)利用导数解决曲线的切线问题,从而解出a,b的值
(2)通过构造新函数的方法找到证明不等式的突破口。
易错点
不等式证明如何构造新函数
扫码查看完整答案与解析
















