等差数列的性质及应用
共237题

· 等差数列的性质及应用

等差数列的性质及应用
共237题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

3．已知等差数列中，是方程的两根，则（）

A- 2014

B- 1007

C1007

D2014

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用等差数列的前n项和及其最值

题型：简答题

简答题 · 18 分

23.一青蛙从点开始依次水平向右和竖直向上跳动，其落点坐标依次是，(如图所示，坐标以已知条件为准)，表示青蛙从点到点所经过的路程。

（1）若点为抛物线准线上一点，点均在该抛物线上，并且直线经过该抛物线的焦点，证明；

（2）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且,试写出(请简要说明理由)；

（3）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且,求数列和的通项公式。

正确答案

（1）设，由于青蛙依次向右向上跳动，

所以，，由抛物线定义知：

（2）依题意，

随着的增大，点无限接近点

横向路程之和无限接近，纵向路程之和无限接近

所以 =

(注：只要能说明横纵坐标的变化趋势，用文字表达也行)

（3）设点，由题意，的坐标满足如下递推关系：

，且

其中，∴，

∴是以为首项，为公比的等比数列，

∴，

即当为偶数时，，

又，

∴当为奇数时，

∴，；

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用数列的极限数列与解析几何的综合抛物线的标准方程和几何性质

题型：填空题

填空题 · 4 分

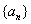
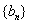
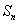
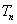
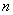
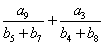
10．已知等差数列，的前n项和分别为，，若对于任意的自然数，都有则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

题型：简答题

简答题 · 12 分

19．已知正项数列前n项和为，首项为，且成等差数列。

（1）求数列的通项公式；

（2）若，为数列的前n项和，证明。

正确答案

（1）由题意知，且可得

当时，

当时，，两式相减得，

整理得

所以数列是首项2，公比为2的等比数列。

（2）

；

两式相减得

所以

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an等差数列的性质及应用错位相减法求和数列与不等式的综合

题型：简答题

简答题 · 12 分

16．设是公差大于零的等差数列，已知，．

（Ⅰ）求的通项公式；

（Ⅱ）设是以函数的最小正周期为首项，以为公比的等比数列，求数列的前项和．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：单选题

单选题 · 5 分

3．在等差数列中，，表示数列的前项和，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用等差数列的前n项和及其最值

题型：填空题

填空题 · 4 分

6. 设等差数列的公差为正，若，则（）.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用

题型：单选题

单选题 · 5 分

15. 若抛物线上不同三点的横坐标的平方成等差数列，那么这三点 ( )

A到原点的距离成等差数列

B到轴的距离成等差数列

C到轴的距离成等差数列

D到焦点的距离的平方成等差数列

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的判断与证明等差数列的性质及应用抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

7．等差数列中．＜ 0 ， 0 ．且，为数列的前n项和，则使> 0 的n的最小值为（）

A2 1

B20

C10

D11

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

题型：填空题

填空题 · 4 分

14．已知等差数列的首项为24，公差为，则当n=（）时，该数列的前n项和取得最大值。

正确答案

n=12或13

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

继续学习学习下一知识点

下一知识点 : 等差数列的前n项和及其最值

百度题库 > 高考 > 文科数学 > 等差数列的性质及应用

扫码查看完整答案与解析