等差数列的性质及应用
共237题

· 等差数列的性质及应用

等差数列的性质及应用
共237题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

9．已知等差数列中，，记数列的前项和为，若，对任意的成立，则整数的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项等差数列的性质及应用数列与不等式的综合

题型：单选题

单选题 · 5 分

3．在等差数列中，若，则为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用

题型：单选题

单选题 · 5 分

7．已知数列的前项和，正项等比数列中，，，则（）

An-1

B2n-1

Cn-2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质由递推关系式求数列的通项公式等差数列的性质及应用等比数列的基本运算

题型：简答题

简答题 · 14 分

19．已知数列是公差不为零的等差数列，，且、、成等比数列．

（1）求数列的通项公式；

（2）设，数列的前项和为，求证：．

正确答案

（1）解：设数列的公差为（），由已知得：

即：

解之得：

，（）

（2）证明: ∵．

，　　　 ①

．　　②

①－②得:

得，

∵，

∴．

，

∴．

而，所以最小

又，所以

综上所述，．

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：单选题

单选题 · 5 分

5．在等差数列中，前15项和，则（）

C12

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用等差数列的前n项和及其最值

题型：简答题

简答题 · 18 分

23．已知数列中，且点在直线上

（1）求数列的通项公式；

（2）若函数求函数的最小值；

（3）设表示数列的前项和．试问：是否存在关于的整式，使得对于一切不小于2的自然数恒成立？若存在，写出的解析式，并加以证明；若不存在，试说明理由。

正确答案

相加得：，n≥2

所以。故存在关于n的整式g（x）=n，使得对于一切不小于2的自然数n恒成立。

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值函数恒成立、存在、无解问题由递推关系式求数列的通项公式等差数列的性质及应用数列与解析几何的综合

题型：填空题

填空题 · 4 分

16．第一行：1

第二行：2 3 4

第三行：3 4 5 6 7

第四行：4 5 6 7 8 9 10

… …

从上图观察可得第（）行的各数之和等于．

正确答案

1006

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：单选题

单选题 · 5 分

9．已知为等差数列，++=105，=99，以表示的前项和，则使得达到最大值的是（）

A21

B20

C19

D18

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：填空题

填空题 · 5 分

13．已知{an}为等差数列，Sn为其前n项和，若，，则a2=______， =_______。

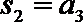
正确答案

;

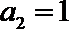
解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：单选题

单选题 · 5 分

4．在等差数列中，，则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

运用诱导公式化简求值等差数列的性质及应用

继续学习学习下一知识点

下一知识点 : 等差数列的前n项和及其最值

百度题库 > 高考 > 文科数学 > 等差数列的性质及应用

扫码查看完整答案与解析