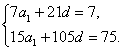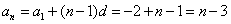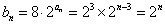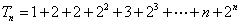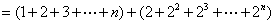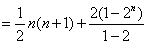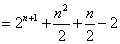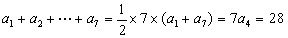- 等差数列的性质及应用
- 共237题
1
题型:简答题
|
设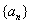
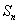
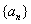
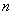
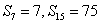
(1)求数列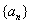
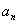
(2)设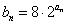
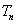
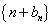
正确答案
见解析。
解析
(1)设等差数列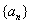
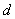
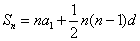
∵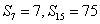
∴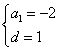
∴
(2)由(1)得
∴
知识点
等差数列的性质及应用
1
题型:简答题
|
已知等差数列{an}的前n项和Sn满足S3=0,S5=-5.
(1)求{an}的通项公式;
(2)求数列
正确答案
(1)an=2-n.
(2)
解析
(1)设{an}的公差为d,则Sn=
由已知可得
解得a1=1,d=-1.
故{an}的通项公式为an=2-n.
(2)由(1)知

从而数列
=
知识点
等差数列的性质及应用
1
题型:
单选题
|
如果等差数列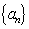
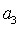
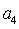
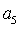
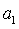
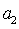
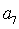
正确答案
C
解析
∵ 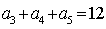
知识点
等差数列的性质及应用
1
题型:
单选题
|
已知等差数列{

正确答案
A
解析
略
知识点
等差数列的性质及应用等差数列的前n项和及其最值
1
题型:简答题
|
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列。
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
正确答案
(1)an=-2n+27.
(2)Sn=-3n2+28n.
解析
(1)设{an}的公差为d.
由题意,
即(a1+10d)2=a1(a1+12d)。
于是d(2a1+25d)=0.
又a1=25,所以d=0(舍去),d=-2.
故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列。
从而Sn=

知识点
等差数列的性质及应用等差数列的前n项和及其最值
下一知识点 : 等差数列的前n项和及其最值
扫码查看完整答案与解析