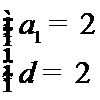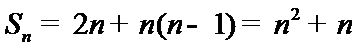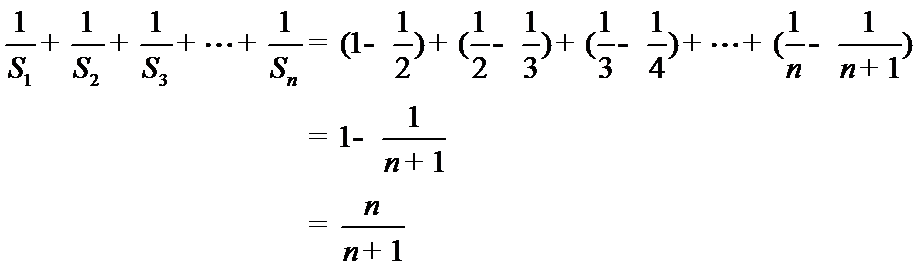- 等差数列的性质及应用
- 共237题
8.已知等差数列{an}的前n项和为Sn,若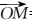
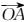
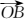
正确答案
2015
解析
若O、A、B、M为平面内四点,则A、B、M三点在一条直线上,当且仅当存在一对实数m、n,使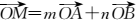
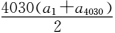
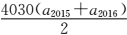
知识点
5.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3 ,则S5 = (
正确答案
解析
根据关系式a1+a3+a5=3,得到a1+2d=1,,S5=5a1+10d,所以S5=5(a1+2d)=5,所以本题选A
考查方向
本题主要考查等差数列项数和项之间的关系,属于中档题,是高考的热点。
解题思路
通过前三项奇数项关系式,求出等差数列的首项和公差,利用等差数列前n项和求和公式求解。
易错点
等差数列项数和项概念混淆。
知识点
12.



且

正确答案
8
解析


所以

所以

所以填8
考查方向
解题思路
先求出a7的值,然后再求答案
易错点
不转换建立关系,直接算
知识点
17.已知等差
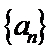
(Ⅰ)求数列
(Ⅱ)若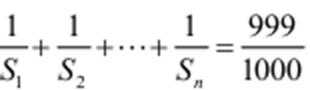
正确答案
(Ⅰ)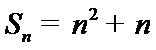
解析
(Ⅰ)设等差数列
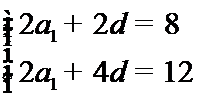
所以
(Ⅱ)由(Ⅰ)得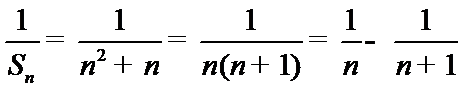
所以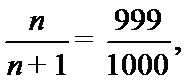
考查方向
解题思路
解题步骤如下:设该数列的公差,根据题意建立方程组,求出首项和公差,可求出数列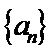
易错点
1、本题在裂项时容易发生错误。2、考生不理解裂项求和方法,或方程看似很复杂,导致题目无法进行。
知识点
13.若数a1,a2,a3,a4,a5的标准差为2,则数3a1﹣2,3a2﹣2,3a3﹣2,3a4﹣2,3a5﹣2的方差为 .
正确答案
36
解析
试题分析:因为a1,a2,a3,a4,a5的标准差为2,所以其方差为4,设数据a1,a2,a3,a4,a5的平均数为



考查方向
解题思路
根据标准差求出方差,再利用均值与方差的性质求出所给数据的方差。
易错点
对方差与标准差的概念不清楚导致出错。
知识点
扫码查看完整答案与解析