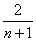- 等差数列的性质及应用
- 共237题
已知函数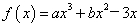
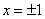
(1)求函数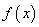
(2)若过点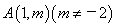

正确答案
见解析。
解析
(1)


即
(2)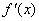
过点A可作曲线的两条切线,所以点A(1,m)不在曲线上。
设切点为M(x0,y0),则点M的坐标满足
因为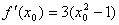


因为过点A(1,m)可作曲线的两条切线,
所以关于x0方程
设g(x0)= 

由g′(x0)=0,得x0=0或x0=1.
所以g(x0)在(-∞,0),(1,+∞)上单调递增,在(0,1)上单调递减,
所以函数g(x0)=
所以关于x0方程
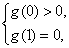

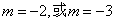
故所求的实数m的值为2或3.
知识点
在数列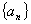

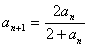
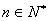

正确答案
解析
略
知识点
在等差数列





正确答案
解析
设公差为d,由




所以
知识点
给定正整数






(1)判断数列

(2)若


(3)设


均构成“Γ数列”,求

正确答案
见解析
解析
(1)①因为


②因为


所以数列

(2)反证法证明:
假设存在某项

设

所以

这与“
(3)由(2)问可知
①当

②当
由“

整理得
显然当
所以


综上讨论可知

知识点
已知



正确答案
解析
知识点
在等差数列


正确答案
解析
设公差为





知识点
等差数列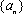
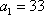
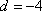

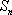
正确答案
解析
由得到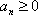
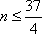

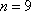
知识点
已知数列

(1)求数列
(2)设数列


正确答案
见解析。
解析
(1)由


得

(2)由

因为
所以


所以 
知识点
等差数列{an}中,a3=5,a10=-9. 求:
(1)数列{an}的通项公式;
(2)数列{an}的前n项和Sn.
正确答案
见解析
解析
(1)由题意得:
解得:
所以数列的通项公式为
(2)

知识点
设等差数列




正确答案
45
解析
由
得
知识点
扫码查看完整答案与解析