- 等差数列的性质及应用
- 共237题
在数列



(1)求数列
(2)设数列



正确答案
见解析。
解析
(1)∵



∴
(2)由(1)知,
∴
∴
………………………………………………………………………………10分

知识点
已知数列


(1)求数列

(2)设



正确答案
见解析。
解析
(1)由已知,得

又首项

所以
又

(2)
当

当
知识点
如图,








正确答案
解析
由割线定理知


知识点
已知数列{an}中,Sn为前n项的和,2Sn=3an-1。
(1)求an;
(2)若数列{bn}满足

正确答案
见解析。
解析
知识点
已知等差数列




(1)求数列

(2)证明
正确答案
见解析。
解析
知识点
等差数列{an}的前10项和为10,前20项和为30,则其前30项和等于 。
正确答案
60
解析
略
知识点
已知等差数列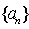


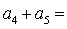
正确答案
解析
略
知识点
设等差数列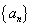




正确答案
解析
略
知识点
在等差数列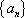

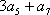
正确答案
解析
略
知识点
各项均为正数的数列





(1)求数列
(2)若







正确答案
见解析。
解析
(1)由

即
又



由


故数列

(2)因



所以

∴


所以
所以对任意的

知识点
扫码查看完整答案与解析