- 等差数列的性质及应用
- 共237题
设数列






(1)求数列
(2)若


正确答案
见解析。
解析
(1)因为点


当



又当

所以




⑵由⑴知,







所以,数列

知识点
已知数列


(1)求



(2)设


正确答案
见解析。
解析
(1)设


解得

所以

(2)∵
∴
∵
∴数列
知识点
已知数列



正确答案
解析
知识点
已知数列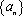
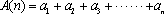
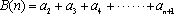
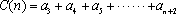
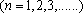
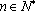
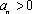
(1)若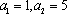
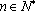
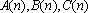
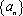
(2)证明:数列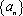
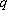
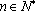
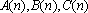
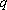
正确答案
见解析
解析
解析:(1)
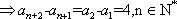
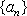
(2)(必
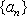
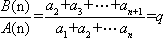
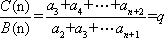
(充分性):若对于任意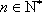
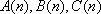
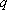
则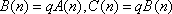
于是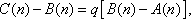
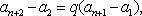
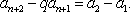
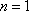
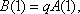
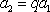
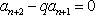
因为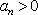
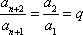

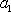
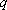
综上,数列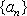
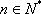

知识点
数列




(1)求数列
(2)若





成立,求实数
正确答案
见解析。
解析
(1)当

当


∴

∴
(2)









知识点
数列



(1)求数列
(2)若


正确答案
见解析
解析
解:(1)由已知得

又

(2)由(1)得,
所以

知识点
已知数列



且
(1)求数列
(2)求证:数列
正确答案
见解析
解析
(1)由已知

(2)由于
令




① -②得
又
∴数列


知识点
数列




正确答案
7
解析
略
知识点
设等差数列








正确答案
解析
略
知识点
设



正确答案
9
解析
略
知识点
扫码查看完整答案与解析